Edited, memorised or added to reading queue
on 29-May-2019 (Wed)
 |
#Transformations_matière #has-images
Le remplacement d’un atome par un isotope est une technique d’étude intéressante. Cette opération permet en général le marquage d’un atome : le remplacement n’affecte pas (ou peu) la réactivité chimique, mais permet de suivre sans ambiguité le devenir de l’atome. Un exemple est fourni en médecine nucléaire par la TEP (tomographie par émission de positons) ou PET-scan. La technique consiste à utiliser une molécule marquée avec un isotope radioactif. On utilise principalement le fluorodesoxyglucose marqué au fluor 18 (voir figure 2.4). Le fluor 18 est un atome qui se désintègre (radioactivité) en emettant un positon selon le bilan nucléaire suivant : \({}_{9}^{18}F~=~{}_{8}^{18}O~+~{}_{1}^{0}e~+~{}_{0}^{0}{\nu_e}\) . Le fluorodesoxyglucose est injecté au patient. Un tissu organique anormal (par exemple, une tumeur cancéreuse) consomme plus de glucose qu’un tissu sain et concentre donc la radioactivité. Le repérage de zones concentrées de radioactivité permet ainsi la localisation des tissus malins.
|
| status | not read | reprioritisations | ||
|---|---|---|---|---|
| last reprioritisation on | suggested re-reading day | |||
| started reading on | finished reading on |
|
#Transformations_matière
On ne peut pas connaître avec exactitude le rayon d’un atome car on ne peut pas déterminer avec certitude la dimension du nuage électronique. On peut cependant mesurer la distance qui sépare les noyaux des atomes d’une molécule donnée, ou la distance qui sépare les noyaux de deux atomes voisins d’un échantillon métallique solide (utilisation d’expérience de diffraction de rayons X). Par exemple, la distance entre deux atomes de cuivre est égale à 256 pm dans Cu(s) : on définit le rayon du cuivre (dit rayon métallique) comme la demi-longueur de la distance entre deux atomes de cuivre (128 pm). La distance entre deux atomes de chlore dans la molécule de dichlore vaut 198 pm : on définit le rayon du chlore (dit rayon covalent car les atomes sont liés par liaison covalente) comme la demi-longueur de la distance entre deux atomes de chlore (99 pm). Ici l’ordre de grandeur des rayons déterminés est compris entre 40 et 300 pm. Le rayon ionique d’un élément chimique est sa contribution à la distance entre deux ions voisins d’un solide ionique (solide constitué par une association de cations et d’anions). En effet, la distance entre les noyaux d’un cation et d’un anion voisins est égale à la somme des deux rayons ioniques. À titre d’exemple, la distance séparant les noyaux des ions Mg2+ et O2– dans MgO(s) est égale à 205 pm, cette distance est égale à la somme des rayons ioniques r(Mg2+) + r(O2−). Le rayon ionique relatif à un élément chimique peut être comparé au rayon de l’atome relatif au même élément chimique (sachant que le rayon atomique est soit le rayon covalent, soit le rayon métallique selon la mesure réalisée), et on constate alors que : le rayon d’un cation est plus petit que le rayon de l’atome, tandis que le rayon d’un anion est plus grand que le rayon de l’atome. |
| status | not read | reprioritisations | ||
|---|---|---|---|---|
| last reprioritisation on | suggested re-reading day | |||
| started reading on | finished reading on |
|
#Transformations_matière
Bien avant le XXème siècle, de nombreux phénomènes physiques et chimiques sont déjà expliqués par les savants. En effet :
Néanmoins, quelques phénomènes, pudiquement (ou hypocritement) considérés comme marginaux ne sont pas expliqués, en particulier le comportement du rayonnement du corps noir dans le domaine ultra-violet (catastrophe ultra-violette). Cette observation sera à l’origine d’un nouveau courant de pensée, d’une physique et d’une chimie nouvelle et puissante : la chimie quantique, au début du XXème siècle. |
| status | not read | reprioritisations | ||
|---|---|---|---|---|
| last reprioritisation on | suggested re-reading day | |||
| started reading on | finished reading on |
|
#Transformations_matière
Il existe deux modèles complémentaires, tous les deux valables, pour décrire les phénomènes lumineux : la théorie ondulatoire de la lumière, et la théorie corpusculaire de la lumière.
|
| status | not read | reprioritisations | ||
|---|---|---|---|---|
| last reprioritisation on | suggested re-reading day | |||
| started reading on | finished reading on |
 |
#Transformations_matière #has-images
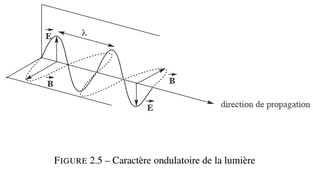
La théorie ondulatoire de la lumière décrit les phénomènes lumineux comme la propagation d’un champ électromagnétique, c’est-à-dire à la fois un champ électrique \(\overrightarrow{E(M,t)}\) et un champ magnétique \(\overrightarrow{B(M,t)}\) , sachant que ces 2 vecteurs sont tous les 2 orthogonaux à la direction de propagation du champ électromagnétique. Ces ondes électromagnétiques sont dans la majorité des cas des ondes progressives (couplage temps/espace) se propageant à la vitesse c = 3 . 108 m·s-1 dans le vide. La lumière émise par les atomes est décrite par une onde électromagnétique monochromatique dont la dépendance temporelle est en cos(ωt). De plus, cette onde électromagnétique monochromatique est caractérisée par :
De plus, la distance parcourue par la lumière durant une période T, à la vitesse c dans le vide, est égale à sa longueur d'onde. Ainsi, on a : \(\lambda~=~c \cdot T ~=~ {c \over \nu}\) . |
| status | not read | reprioritisations | ||
|---|---|---|---|---|
| last reprioritisation on | suggested re-reading day | |||
| started reading on | finished reading on |
|
#Transformations_matière
La théorie corpusculaire de la lumière décrit les phénomènes lumineux comme la propagation d’une population de photons, qui sont des particules sans masse se déplaçant à la vitesse de la lumière c dans le vide. À chaque particule est associée une énergie E.
|
| status | not read | reprioritisations | ||
|---|---|---|---|---|
| last reprioritisation on | suggested re-reading day | |||
| started reading on | finished reading on |
|
#Transformations_matière
Le lien entre les deux théories ondulatoire et corpusculaire de la lumière est obtenu par la relation suivante : \(E~=~h \cdot \nu ~=~h \cdot { c \over \lambda}\) ; avec h la constante de PLANCK (h = 6,62 . 10−34 J·s). E est l’énergie exprimée en joules (J), \(\nu\) est la fréquence en hertz (Hz) , c qui est la vitesse de l'onde électromagnétique dans le vide, et \(\lambda\) sa longueur d'onde.
|
| status | not read | reprioritisations | ||
|---|---|---|---|---|
| last reprioritisation on | suggested re-reading day | |||
| started reading on | finished reading on |
|
B value, computed on the training set, f
|
| status | not read | reprioritisations | ||
|---|---|---|---|---|
| last reprioritisation on | suggested re-reading day | |||
| started reading on | finished reading on |
 |
#Transformations_matière #has-images
Malgré la nature commune du phénomène, l’usage attribue des noms différents au rayonnement électromagnétique suivant la longueur d’onde (et donc l’énergie véhiculée), nous re- tiendrons le résultat important suivant : le rayonnement visible possède une longueur d’onde comprise entre 400 nm (couleur violette) et 750 nm (couleur rouge). Nous rappelons à la figure 2.6 le spectre électromagnétique (nom attribué au rayonnement en fonction de la longueur d’onde ou de la fréquence).
|
| status | not read | reprioritisations | ||
|---|---|---|---|---|
| last reprioritisation on | suggested re-reading day | |||
| started reading on | finished reading on |
|
#Transformations_matière
Les électrons liés au noyau possèdent une propriété particulière : leur énergie est quantifiée. Ce terme signifie que l’énergie possédée par un électron ne peut pas prendre toutes les valeurs possibles mais un nombre limité de valeurs (des valeurs dites discrètes par opposition à continues).
|
| status | not read | reprioritisations | ||
|---|---|---|---|---|
| last reprioritisation on | suggested re-reading day | |||
| started reading on | finished reading on |
|
#Transformations_matière
L'expérience de FRANCK et HERTZ, dont les résultats ont été présentés en 1924, a été une expérience décisive pour montrer la quantification de l’énergie électronique dans l’atome. Elle consiste à bombarder de la vapeur de mercure par des électrons accélérés sous une différence de potentiel pouvant atteindre quelques dizaines de volts. D’un point de vue pratique un filament chauffé (jouant le rôle de cathode) émet des électrons qui sont accélérés par une anode (qui est ici une grille) portée à un potentiel très positif. Puis on mesure l'intensité électrique i(t) du courant électrique arrivant sur la grille en fonction de la tension accélératrice U(t) appliquée entre le filament et la grille. Le résultat expérimental est le suivant lorsque l'on trace la caractéristique courant-tension du dispositif cathode-anode :
Et lorsque la tension U(t) augmente jusqu’à 20 V la situation précédente se répète pour des intervalles analogues. L’expérience est interprétée de la façon suivante :
|
| status | not read | reprioritisations | ||
|---|---|---|---|---|
| last reprioritisation on | suggested re-reading day | |||
| started reading on | finished reading on |
 |
#Transformations_matière #has-images
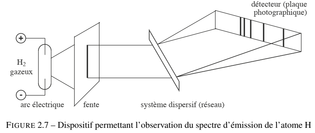
L’observation du spectre d’émission de l’atome d’hydrogène est aussi une manifestation importante de la propriété de quantification de l’énergie électronique. Nous appelons spectre d’émission de l’atome d’hydrogène l’ensemble des ondes électromagnétiques pouvant être émises par un atome d’hydrogène excité (ayant reçu un excédent d’énergie). Celui-ci est obtenu expérimentalement dans un tube à décharge contenant du dihydrogène et muni de deux électrodes métalliques (voir figure 2.7). Le tube contient du dihydrogène sous faible pression (de l’ordre de 10-3 bar), une décharge est opérée et ionise partiellement le dihydrogène H2. Les ions générés sont accélérés par la différence de potentiel régnant entre les deux électrodes et percutent à grande vitesse les molécules de dihydrogène en provoquant la dissociation en atomes d’hydrogène, ainsi que l’excitation des atomes formés. Les atomes ne gardent que très peu de temps cet excédent d’énergie : ils le libèrent sous forme de lumière (on dit qu’ils se désexcitent). Le rayonnement émis est constitué d’une série de raies de longueurs d’onde différentes. C’est le spectre |
| status | not read | reprioritisations | ||
|---|---|---|---|---|
| last reprioritisation on | suggested re-reading day | |||
| started reading on | finished reading on |
 |
#Transformations_matière #has-images
Constats expérimentaux du spectre d’émission de l’atome d’hydrogène :
|
| status | not read | reprioritisations | ||
|---|---|---|---|---|
| last reprioritisation on | suggested re-reading day | |||
| started reading on | finished reading on |
 |
#Classification_périodique_des_éléments_chimiques #has-images
De façon symétrique, il est possible d’observer le spectre d’absorption d’un atome. Pour obtenir le spectre d’absorption d’un atome, un échantillon contenant des atomes de cet élément à l’état gazeux est soumis à un rayonnement incident. Ce rayonnement incident est constitué par un spectre continu (il contient toutes les longueurs d’onde d’une fraction du spectre électromagnétique). Le rayonnement est analysé après son passage dans l’échantillon ; il ne contient plus les longueurs d’onde qui ont été absorbées (ces longueurs d’onde sont les mêmes que celles mises en évidence par un spectre d’émission du même atome). En pratique, un spectre d’absorption se présente sous forme d’un spectre continu dont certaines radiations sont manquantes (absorbées). Les radiations absorbées apparaissent sous forme de fines raies noires ( voir un exemple de spectre de raies sur la figure 2.8 ). De façon tout à fait empirique, les spectroscopistes ont constaté que le nombre d’onde σ des radiations émises (ou absorbées) dans le cas de l’atome d’hydrogène (et plus précisément l'isotope 11H) vérifie la relation suivante, dite de RITZ-RYDBERG : \(\sigma~=~R_{H} \cdot \left ( { 1 \over n^2}~-~ { 1 \over p^2 } \right )\) avec :
La constante RH de RYDBERG ne s’applique qu’au cas du spectre d’émission de l’isotope 11H et ne sera en aucun cas généralisable à un autre atome ou isotope. Par ailleurs, il faut prendre garde aux unités, si la constante RH est en cm-1, alors le nombre d’onde \(\sigma\) sera en cm-1 (sachant que pour obtenir un nombre d’onde en m-1 il convient d’utiliser la conversion 1 cm-1 = 100 m-1 ).
|
| status | not read | reprioritisations | ||
|---|---|---|---|---|
| last reprioritisation on | suggested re-reading day | |||
| started reading on | finished reading on |
|
#Classification_périodique_des_éléments_chimiques
Les processus d’absorption et d’émission d'un atome sont bien décrits par la version corpusculaire de la lumière : c'-à-d par des absorption et émission de photons. BOHR énonce en 1913 deux postulats qui expliquent la forme du spectre d’émission de l’atome d’hydrogène :
|
| status | not read | reprioritisations | ||
|---|---|---|---|---|
| last reprioritisation on | suggested re-reading day | |||
| started reading on | finished reading on |
 |
#Classification_périodique_des_éléments_chimiques #has-images
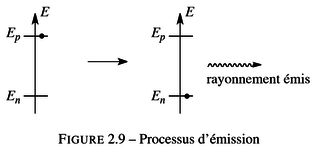
Au cours du processus d’émission d'énergie par un atome, un électron d’énergie Ep peut revenir à l’état d’énergie En inférieure (voir figure 2.9), car il abandonnera son excédent d’énergie par émission d’un photon. Le photon émis sera tel que la variation d'énergie vaut : \({\Delta}E~=~E_{p}~-~E_{n}~=~h \cdot \nu ~=~h \cdot { c \over \lambda }\) .
|
| status | not read | reprioritisations | ||
|---|---|---|---|---|
| last reprioritisation on | suggested re-reading day | |||
| started reading on | finished reading on |
 |
#Classification_périodique_des_éléments_chimiques #has-images
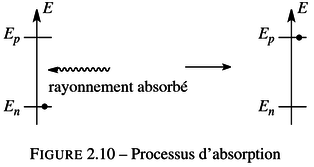
Au cours du processus d’émission d'énergie par un atome, un électron d’énergie En peut monter à l’état d’énergie Ep supérieure (voir figure 2.10), car il gagnera un excédent d’énergie par absorption d’un photon par l'atome. Le photon absorbé sera tel que la variation d'énergie vaut : \({\Delta}E~=~E_{p}~-~E_{n}~=~h \cdot \nu ~=~h \cdot { c \over \lambda }\) .
|
| status | not read | reprioritisations | ||
|---|---|---|---|---|
| last reprioritisation on | suggested re-reading day | |||
| started reading on | finished reading on |
 |
#Classification_périodique_des_éléments_chimiques #has-images
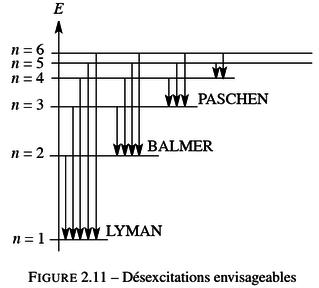
L’énergie de l’électron lié à l’atome (dans le cas précis de l’atome d’hydrogène) ne peut prendre que les valeurs : En = − 13.6 /(n2) (en eV) avec n qui est un nombre entier positif. Rappelons la valeur de l’électron-volt (eV) : 1 eV = 1,6 . 10−19 J. L’état d’énergie E = 0 (qui correspond à n → ∞) correspond à un électron libre de toute contrainte électrostatique (situé à l’infini du noyau de l’atome et sans énergie cinétique). Il s’agit donc de l’électron correspondant à un atome ionisé. L’état fondamental est l’état électronique d’énergie minimale correspondant à n = 1 (l’énergie d’un électron de l’atome d’hydrogène, dans son état fondamental, est −13,6 eV). Les états correspondant à un n supérieur sont qualifiés d’états excités (et correspondent à l’état d’un électron excité, ayant reçu un excédent d’énergie). Une série de raies d'émission est interprétée comme la manifestation de désexcitations, ayant toutes en commun le retour vers un niveau d’énergie En donné. Ainsi les désexcitations vers le niveau fondamental constituent la série de LYMAN, les transitions vers n = 2, 3 et 4 constituent respectivement les séries de BALMER, PASCHEN et BRACKETT. Chaque série est constituée d’un grand nombre de raies dont les longueurs d’onde se rapprochent et tendent vers une longueur d’onde limite (voir la figure 2.11). Les résultats et raisonnements précédents sont généralisables aux ions hydrogénoïdes. |
| status | not read | reprioritisations | ||
|---|---|---|---|---|
| last reprioritisation on | suggested re-reading day | |||
| started reading on | finished reading on |
|
#Classification_périodique_des_éléments_chimiques
Un ion hydrogénoïde est un ion ne comportant qu’un seul électron (et Z protons). À titre d’exemple, citons l’ion Li2+ . En effet le lithium Li possède 3 protons (Z = 3) et donc 3 électrons à l’état atomique ; ainsi l’ion Li2+ possède un seul électron (il a perdu 2 charges électriques négatives), il s’agit bien d’un ion hydrogénoïde. De même nous pouvons vérifier que l’ion He+ est un ion hydrogénoïde (Z = 2 pour l’hélium He). De façon similaire à l’atome d’hydrogène, l’énergie de l’électron dans un ion hydrogénoïde ( de numéro atomique Z ) est quantifiée. Les niveaux d’énergie prennent dans ce cas la forme : \(E_{n}~=~- \left( 13,6 \over {n^2} \right ) \cdot Z^2\) (en électron-volts). Ne pas oublier le facteur Z2 . |
| status | not read | reprioritisations | ||
|---|---|---|---|---|
| last reprioritisation on | suggested re-reading day | |||
| started reading on | finished reading on |
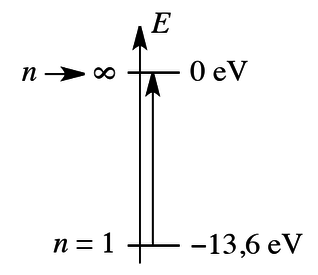 |
#Classification_périodique_des_éléments_chimiques #has-images
Processus d’ionisation : Calculer l’énergie minimale à fournir à un atome d’hydrogène (initialement dans son état fondamental) pour provoquer une ionisation (on parle alors d’énergie d’ionisation). Réponse : L’énergie fournie sera absorbée si elle provoque une transition électronique (cas de l’électron lié). Pour procéder à une ionisation il faut au minimum provoquer une transition entre l’état fondamental (E = −13,6 eV, n = 1) et l’état ionisé (E = 0 eV, n →∞). La transition est schématisée à la figure ci-dessus. L’énergie à fournir (et susceptible d’être absorbée) est 13,6 eV, soit 21,8 . 10-19 J. Ceci peut être converti en J·mol-1 ou kJ·mol-1 : 21,8 . 10-19 J = 21,8 . 10-19 × NA = 1,3 . 106 J·mol-1 = 1.300 kJ·mol-1. NA = 6,02 . 1023 mol-1 est la constante d’AVOGADRO, et il correspond au nombre d’atomes d’hydrogène que l’on trouve dans une mole d’atomes d’hydrogène. |
| status | not read | reprioritisations | ||
|---|---|---|---|---|
| last reprioritisation on | suggested re-reading day | |||
| started reading on | finished reading on |
 |
#Classification_périodique_des_éléments_chimiques #has-images
Transitions extrêmes d’une série de raies : Calculer la longueur d’onde des deux raies extrêmes de la série de LYMAN (correspondant à un retour sur le niveau d’énergie n = 1). Réponse : Schématisons ces deux transitions (sur la figure ci-contre) : la plus grande énergie émise correspond à une transition entre l’état E = 0 eV (n → ∞) et l’état E1 = −13,6 eV (n = 1), soit une énergie de 13,6 eV. La plus faible énergie émise correspond à la transition entre l’état E2 = −13,6/4 = −3,4 eV (n = 2) et l’état E1 = −13,6 eV (n = 1), soit une énergie de 10,2 eV . Or la variation d'énergie dans un spectre de raies d'émission ou d'absorption est obtenue grâce à la relation \(E~=~h \cdot { c \over \lambda }\) , et donc on a de manière équivalente \(\lambda ~=~{ { h \cdot c } \over E}\) . Ainsi, on obtient :
Ces 2 rayonnements correspondent alors au domaine ultra-violet. |
| status | not read | reprioritisations | ||
|---|---|---|---|---|
| last reprioritisation on | suggested re-reading day | |||
| started reading on | finished reading on |
|
#Classification_périodique_des_éléments_chimiques
Raies du domaine visible : Combien de raies de la série de BALMER appartiennent au domaine visible ? Quelles sont leurs couleurs respectives ? (On rappelle que la série de BALMER concerne des transitions vers le niveau n = 2). Réponse : Nous devons calculer les longueurs d’onde des premières raies.
|
| status | not read | reprioritisations | ||
|---|---|---|---|---|
| last reprioritisation on | suggested re-reading day | |||
| started reading on | finished reading on |
|
#Classification_périodique_des_éléments_chimiques
L’énergie des électrons est une grandeur quantifiée dans tout atome, ion ou molécule. Cette propriété est utilisée en spectroscopie UV-visible. L’interaction des radiations lumineuses et de la matière dans le domaine s’étendant du proche ultra-violet au très proche infra-rouge (entre 180 nm et 1100 nm) a une grande importance en analyse quantitative. En effet, une absorption de rayonnement lumineux d’énergie \(E~=~h \cdot \nu\) est possible lorsqu’elle engendre une transition entre états d’énergie, c’est-à-dire lorsque : \({\Delta}E ~=~ h \cdot \nu\) avec ∆E la différence d’énergie entre deux énergies possibles. L’ordre de grandeur des différentes énergies électroniques possibles (quantifiées) est telle qu’une modification de l’état d’énergie des électrons entraîne l’absorption d’une radiation appartenant au domaine UV- visible. À titre d’exemple, une transition électronique est observée dans le cas de l’ion permanganate MnO4– après absorption de radiations lumineuses de longueurs d’onde comprises entre 450 nm et 600 nm, avec un maximum d’absorption mesuré pour une longueur d’onde égale à 525 nm. On observe des bandes d’absorption et non plus des raies d’absorption. L’ion est ici en solution et n’est plus en phase gaz.
|
| status | not read | reprioritisations | ||
|---|---|---|---|---|
| last reprioritisation on | suggested re-reading day | |||
| started reading on | finished reading on |
|
#Classification_périodique_des_éléments_chimiques
La loi de BEER-LAMBERT permet d’évaluer la capacité d’absorption d’un rayonnement lumineux par une substance susceptible de subir une transition entre états électroniques. Cette loi s'écrit sous la forme : \(A~=~ \log \left ( {I_0} \over I \right ) ~=~ {\epsilon} \cdot l \cdot c\) ; avec :
De plus, l'absorptivité molaire \(\epsilon\) dépend de :
|
| status | not read | reprioritisations | ||
|---|---|---|---|---|
| last reprioritisation on | suggested re-reading day | |||
| started reading on | finished reading on |
|
#Classification_périodique_des_éléments_chimiques
L'absorbance A d'un rayonnement UV-visible ( c'-à-d dans le domaine de l'utra-violet ou dans le domaine visible ) par une susbtance absorbante est généralement calculée de la façon suivante : on commence par construire une courbe d’étalonnage A = f (c) à partir de solutions de concentrations molaires connues en susbtance absorbante. Cette courbe est le plus souvent assimilable à une droite pour des solutions diluées. Elle permet ensuite de déduire une concentration inconnue cX par la mesure de son absorbance AX et par l'utilisation de la relation d’étalonnage A = f (c). Dans le cas d'une solution qui contient plusieurs substances i absorbantes qui absorbent le même rayonnement pour une même longueur d’onde de la radiation incidente, avec un coefficient d’absorption molaire εi et une concentration molaire ci de la substance absorbante n°i , la loi de BEER-LAMBERT est additive et s'écrit : \(A~=~ \displaystyle\sum_{i} \left( { {\epsilon_i} \cdot l \cdot c_i} \right )\) . |
| status | not read | reprioritisations | ||
|---|---|---|---|---|
| last reprioritisation on | suggested re-reading day | |||
| started reading on | finished reading on |