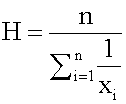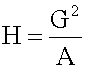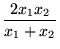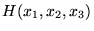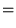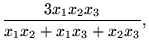Edited, memorised or added to reading queue
on 24-Aug-2019 (Sat)
Do you want BuboFlash to help you learning these things? Click here to log in or create user.
Flashcard 150890360
| status | not learned | measured difficulty | 37% [default] | last interval [days] | |||
|---|---|---|---|---|---|---|---|
| repetition number in this series | 0 | memorised on | scheduled repetition | ||||
| scheduled repetition interval | last repetition or drill |
Parent (intermediate) annotation
Open itConsider the multiplicative model X t = m t × s t × W t .Let Y t denote the time series of logarithms: Y t =log X t .Then Y t =log X t Y t = log(m t × s t × W t ) Y t = log m t +log s t +log W t .
Original toplevel document (pdf)
cannot see any pdfsFlashcard 150890373
| status | not learned | measured difficulty | 37% [default] | last interval [days] | |||
|---|---|---|---|---|---|---|---|
| repetition number in this series | 0 | memorised on | scheduled repetition | ||||
| scheduled repetition interval | last repetition or drill |
Parent (intermediate) annotation
Open itif a multiplicative model is appropriate for the time series X t , then an additive model is appropriate for the time series of logarithms, Y t =log X t .
Original toplevel document (pdf)
cannot see any pdfsFlashcard 150890379
| status | not learned | measured difficulty | 37% [default] | last interval [days] | |||
|---|---|---|---|---|---|---|---|
| repetition number in this series | 0 | memorised on | scheduled repetition | ||||
| scheduled repetition interval | last repetition or drill |
Parent (intermediate) annotation
Open itif a multiplicative model is appropriate for the time series X t , then an additive model is appropriate for the time series of logarithms, Y t =log X t .
Original toplevel document (pdf)
cannot see any pdfsFlashcard 150890385
| status | not learned | measured difficulty | 37% [default] | last interval [days] | |||
|---|---|---|---|---|---|---|---|
| repetition number in this series | 0 | memorised on | scheduled repetition | ||||
| scheduled repetition interval | last repetition or drill |
Parent (intermediate) annotation
Open itif a multiplicative model is appropriate for the time series X t , then an additive model is appropriate for the time series of logarithms, Y t =log X t .
Original toplevel document (pdf)
cannot see any pdfsFlashcard 150890398
| status | not learned | measured difficulty | 37% [default] | last interval [days] | |||
|---|---|---|---|---|---|---|---|
| repetition number in this series | 0 | memorised on | scheduled repetition | ||||
| scheduled repetition interval | last repetition or drill |
Parent (intermediate) annotation
Open itby taking logarithms, a time series for which a multiplicative model is appropriate can be transformed into a time series for which an additive model is appropriate.
Original toplevel document (pdf)
cannot see any pdfsFlashcard 150890411
| status | not learned | measured difficulty | 37% [default] | last interval [days] | |||
|---|---|---|---|---|---|---|---|
| repetition number in this series | 0 | memorised on | scheduled repetition | ||||
| scheduled repetition interval | last repetition or drill |
Parent (intermediate) annotation
Open itTransformations of time series that are commonly used include the power transformations: Y t = X t a , where a = ... 1/4, 1/3, 2, 3, 4, ....
Original toplevel document (pdf)
cannot see any pdfsFlashcard 150890417
| status | not learned | measured difficulty | 37% [default] | last interval [days] | |||
|---|---|---|---|---|---|---|---|
| repetition number in this series | 0 | memorised on | scheduled repetition | ||||
| scheduled repetition interval | last repetition or drill |
Parent (intermediate) annotation
Open itTransformations of time series that are commonly used include the power transformations: Y t = X t a , where a = ... 1/4, 1/3, 2, 3, 4, ....
Original toplevel document (pdf)
cannot see any pdfsFlashcard 150890430
| status | not learned | measured difficulty | 37% [default] | last interval [days] | |||
|---|---|---|---|---|---|---|---|
| repetition number in this series | 0 | memorised on | scheduled repetition | ||||
| scheduled repetition interval | last repetition or drill |
Parent (intermediate) annotation
Open itA simple moving average (or just a moving average) of order (or span) 11 can be written as Y t = 111(X t−5 + ···+ X t + ···+ X t+5 )
Original toplevel document (pdf)
cannot see any pdfsFlashcard 150890436
| status | not learned | measured difficulty | 37% [default] | last interval [days] | |||
|---|---|---|---|---|---|---|---|
| repetition number in this series | 0 | memorised on | scheduled repetition | ||||
| scheduled repetition interval | last repetition or drill |
Parent (intermediate) annotation
Open itA simple moving average (or just a moving average) of order (or span) 11 can be written as Y t = 111(X t−5 + ···+ X t + ···+ X t+5 )
Original toplevel document (pdf)
cannot see any pdfsFlashcard 150890442
| status | not learned | measured difficulty | 37% [default] | last interval [days] | |||
|---|---|---|---|---|---|---|---|
| repetition number in this series | 0 | memorised on | scheduled repetition | ||||
| scheduled repetition interval | last repetition or drill |
Parent (intermediate) annotation
Open itA simple moving average (or just a moving average) of order (or span) 11 can be written as Y t = 111(X t−5 + ···+ X t + ···+ X t+5 )
Original toplevel document (pdf)
cannot see any pdfsFlashcard 150890455
| status | not learned | measured difficulty | 37% [default] | last interval [days] | |||
|---|---|---|---|---|---|---|---|
| repetition number in this series | 0 | memorised on | scheduled repetition | ||||
| scheduled repetition interval | last repetition or drill |
Parent (intermediate) annotation
Open itFor the purpose of smoothing time series, only moving averages for which the order is an odd number will be used. These are said to be centred on the middle value.
Original toplevel document (pdf)
cannot see any pdfsFlashcard 150890471
| status | not learned | measured difficulty | 37% [default] | last interval [days] | |||
|---|---|---|---|---|---|---|---|
| repetition number in this series | 0 | memorised on | scheduled repetition | ||||
| scheduled repetition interval | last repetition or drill |
Parent (intermediate) annotation
Open itWith a suitable degree of smoothing — that is, with a suitable choice of the order of the moving average — the moving average provides an estimate of the trend component m t ; this is denoted mt^
Original toplevel document (pdf)
cannot see any pdfsFlashcard 150890559
| status | not learned | measured difficulty | 37% [default] | last interval [days] | |||
|---|---|---|---|---|---|---|---|
| repetition number in this series | 0 | memorised on | scheduled repetition | ||||
| scheduled repetition interval | last repetition or drill |
Parent (intermediate) annotation
Open itA weighted moving average of order 2q + 1 has the form MA(t)= a −q X t−q + ···+ a −1 X t−1 + a 0 X t + a 1 X t+1 + ···+ a q X t+q , where the weights a j , j = −q, −q +1,... ,
Original toplevel document (pdf)
cannot see any pdfsFlashcard 150890565
| status | not learned | measured difficulty | 37% [default] | last interval [days] | |||
|---|---|---|---|---|---|---|---|
| repetition number in this series | 0 | memorised on | scheduled repetition | ||||
| scheduled repetition interval | last repetition or drill |
Parent (intermediate) annotation
Open itA weighted moving average of order 2q + 1 has the form MA(t)= a −q X t−q + ···+ a −1 X t−1 + a 0 X t + a 1 X t+1 + ···+ a q X t+q , where the weights a j , j = −q, −q +1,... ,q, add up to 1.</
Original toplevel document (pdf)
cannot see any pdfsFlashcard 150890571
| status | not learned | measured difficulty | 37% [default] | last interval [days] | |||
|---|---|---|---|---|---|---|---|
| repetition number in this series | 0 | memorised on | scheduled repetition | ||||
| scheduled repetition interval | last repetition or drill |
Parent (intermediate) annotation
Open itA weighted moving average of order 2q + 1 has the form MA(t)= a −q X t−q + ···+ a −1 X t−1 + a 0 X t + a 1 X t+1 + ···+ a q X t+q , where the weights a j , j = −q, −q +1,... ,q, add up to 1.
Original toplevel document (pdf)
cannot see any pdfsFlashcard 150890577
| status | not learned | measured difficulty | 37% [default] | last interval [days] | |||
|---|---|---|---|---|---|---|---|
| repetition number in this series | 0 | memorised on | scheduled repetition | ||||
| scheduled repetition interval | last repetition or drill |
Parent (intermediate) annotation
Open itl>A weighted moving average of order 2q + 1 has the form MA(t)= a −q X t−q + ···+ a −1 X t−1 + a 0 X t + a 1 X t+1 + ···+ a q X t+q , where the weights a j , j = −q, −q +1,... ,q, add up to 1.<html>
Original toplevel document (pdf)
cannot see any pdfsFlashcard 150890590
| status | not learned | measured difficulty | 37% [default] | last interval [days] | |||
|---|---|---|---|---|---|---|---|
| repetition number in this series | 0 | memorised on | scheduled repetition | ||||
| scheduled repetition interval | last repetition or drill |
Parent (intermediate) annotation
Open itThe weighted moving averages are denoted SA(t) rather than MA(t) when their particular use in smoothing out seasonal variation.
Original toplevel document (pdf)
cannot see any pdfsFlashcard 150890596
| status | not learned | measured difficulty | 37% [default] | last interval [days] | |||
|---|---|---|---|---|---|---|---|
| repetition number in this series | 0 | memorised on | scheduled repetition | ||||
| scheduled repetition interval | last repetition or drill |
Parent (intermediate) annotation
Open itThe weighted moving averages are denoted SA(t) rather than MA(t) when their particular use in smoothing out seasonal variation.
Original toplevel document (pdf)
cannot see any pdfsFlashcard 150890609
| status | not learned | measured difficulty | 37% [default] | last interval [days] | |||
|---|---|---|---|---|---|---|---|
| repetition number in this series | 0 | memorised on | scheduled repetition | ||||
| scheduled repetition interval | last repetition or drill |
Parent (intermediate) annotation
Open itead>The first step is to find an initial estimate of the trend component m t that is not unduly influenced by the seasonal component s t . A reasonable starting point would be to use a simple moving average with order equal to the period T of the seasonal cycle. Such a moving average would smooth out the seasonal variation, as the annual highs and lows would cancel out.<html>
Original toplevel document (pdf)
cannot see any pdfsFlashcard 150890615
| status | not learned | measured difficulty | 37% [default] | last interval [days] | |||
|---|---|---|---|---|---|---|---|
| repetition number in this series | 0 | memorised on | scheduled repetition | ||||
| scheduled repetition interval | last repetition or drill |
Flashcard 150890624
| status | not learned | measured difficulty | 37% [default] | last interval [days] | |||
|---|---|---|---|---|---|---|---|
| repetition number in this series | 0 | memorised on | scheduled repetition | ||||
| scheduled repetition interval | last repetition or drill |
Flashcard 150890643
| status | not learned | measured difficulty | 37% [default] | last interval [days] | |||
|---|---|---|---|---|---|---|---|
| repetition number in this series | 0 | memorised on | scheduled repetition | ||||
| scheduled repetition interval | last repetition or drill |
Parent (intermediate) annotation
Open itThe simple moving average is a weighted moving average in which the weights a j are all equal to (2q +1) −1
Original toplevel document (pdf)
cannot see any pdfsFlashcard 150890954
| status | not learned | measured difficulty | 37% [default] | last interval [days] | |||
|---|---|---|---|---|---|---|---|
| repetition number in this series | 0 | memorised on | scheduled repetition | ||||
| scheduled repetition interval | last repetition or drill |
Parent (intermediate) annotation
Open itOne way to predict tomorrow’s average temperature is to assume it will be the same as today’s.
Original toplevel document (pdf)
cannot see any pdfsFlashcard 150890996
| status | not learned | measured difficulty | 37% [default] | last interval [days] | |||
|---|---|---|---|---|---|---|---|
| repetition number in this series | 0 | memorised on | scheduled repetition | ||||
| scheduled repetition interval | last repetition or drill |
Flashcard 150891005
| status | not learned | measured difficulty | 37% [default] | last interval [days] | |||
|---|---|---|---|---|---|---|---|
| repetition number in this series | 0 | memorised on | scheduled repetition | ||||
| scheduled repetition interval | last repetition or drill |
Parent (intermediate) annotation
Open itt level and no seasonality, 1-step ahead forecasts may be obtained by simple exponential smoothing using the formula x n+1 = αx n + (1 − α)\hat{x}_n where: x n is the observed value at time n, \hat{x}_nand \hat{x}_{n+1}are <span>the 1-step ahead forecasts of X n and X n+1 , and α is a smoothing parameter, 0 ≤ α ≤ 1. The method requires an initial value \hat{x}_1, which is often chosen to be x 1 : \hat{x}_1 = x 1 .<span><body><html>
Original toplevel document (pdf)
cannot see any pdfsFlashcard 150891011
| status | not learned | measured difficulty | 37% [default] | last interval [days] | |||
|---|---|---|---|---|---|---|---|
| repetition number in this series | 0 | memorised on | scheduled repetition | ||||
| scheduled repetition interval | last repetition or drill |
Parent (intermediate) annotation
Open ite obtained by simple exponential smoothing using the formula x n+1 = αx n + (1 − α)\hat{x}_n where: x n is the observed value at time n, \hat{x}_nand \hat{x}_{n+1}are the 1-step ahead forecasts of X n and X n+1 , and α is <span>a smoothing parameter, 0 ≤ α ≤ 1. The method requires an initial value \hat{x}_1, which is often chosen to be x 1 : \hat{x}_1 = x 1 .<span><body><html>
Original toplevel document (pdf)
cannot see any pdfsFlashcard 150891017
| status | not learned | measured difficulty | 37% [default] | last interval [days] | |||
|---|---|---|---|---|---|---|---|
| repetition number in this series | 0 | memorised on | scheduled repetition | ||||
| scheduled repetition interval | last repetition or drill |
Parent (intermediate) annotation
Open itIf a time series X t is described by an additive model with constant level and no seasonality, 1-step ahead forecasts may be obtained by simple exponential smoothing using the formula x n+1 = αx n + (1 − α)\hat{x}_n where:&
Original toplevel document (pdf)
cannot see any pdfsFlashcard 150891023
| status | not learned | measured difficulty | 37% [default] | last interval [days] | |||
|---|---|---|---|---|---|---|---|
| repetition number in this series | 0 | memorised on | scheduled repetition | ||||
| scheduled repetition interval | last repetition or drill |
Parent (intermediate) annotation
Open itIf a time series X t is described by an additive model with constant level and no seasonality, 1-step ahead forecasts may be obtained by simple exponential smoothing using the formula x n+1 = αx n + (1 − α)\hat{x}_n where: x n is the ob
Original toplevel document (pdf)
cannot see any pdfsFlashcard 150891029
| status | not learned | measured difficulty | 37% [default] | last interval [days] | |||
|---|---|---|---|---|---|---|---|
| repetition number in this series | 0 | memorised on | scheduled repetition | ||||
| scheduled repetition interval | last repetition or drill |
Parent (intermediate) annotation
Open itIf a time series X t is described by an additive model with constant level and no seasonality, 1-step ahead forecasts may be obtained by simple exponential smoothing using the formula x n+1 = αx n + (1 − α)\hat{x}_n where: x n is the observed value
Original toplevel document (pdf)
cannot see any pdfsFlashcard 150891035
| status | not learned | measured difficulty | 37% [default] | last interval [days] | |||
|---|---|---|---|---|---|---|---|
| repetition number in this series | 0 | memorised on | scheduled repetition | ||||
| scheduled repetition interval | last repetition or drill |
Parent (intermediate) annotation
Open itIf a time series X t is described by an additive model with constant level and no seasonality, 1-step ahead forecasts may be obtained by simple exponential smoothing using the formula x n+1 = αx n + (1 − α)\hat{x}_n where: x n is the observed value at time n, \ha
Original toplevel document (pdf)
cannot see any pdfsFlashcard 150891041
| status | not learned | measured difficulty | 37% [default] | last interval [days] | |||
|---|---|---|---|---|---|---|---|
| repetition number in this series | 0 | memorised on | scheduled repetition | ||||
| scheduled repetition interval | last repetition or drill |
Parent (intermediate) annotation
Open itIf a time series X t is described by an additive model with constant level and no seasonality, 1-step ahead forecasts may be obtained by simple exponential smoothing using the formula x n+1 = αx n + (1 − α)\hat{x}_n where: x n is the observed value at time n, \hat{x}_nand \hat{x}_{n+1}are the 1-step ahead forecasts of X n and X n
Original toplevel document (pdf)
cannot see any pdfsFlashcard 150891047
| status | not learned | measured difficulty | 37% [default] | last interval [days] | |||
|---|---|---|---|---|---|---|---|
| repetition number in this series | 0 | memorised on | scheduled repetition | ||||
| scheduled repetition interval | last repetition or drill |
Flashcard 150891359
| status | not learned | measured difficulty | 37% [default] | last interval [days] | |||
|---|---|---|---|---|---|---|---|
| repetition number in this series | 0 | memorised on | scheduled repetition | ||||
| scheduled repetition interval | last repetition or drill |
Parent (intermediate) annotation
Open itIf a time series X t is described by an additive model with constant level and no seasonality, 1-step ahead forecasts may be obtained by simple exponential smoothing using the formula \(\hat{x}_{n+1}\)= αx n + (1 − α)\(\hat{x}_n\) where: x n is the observed value at time n, \(\hat{x}_n\)and \(\hat{x}_{n+1}\)are the 1-step ahead forecasts of X n and X n+1 , and α is a smoothing parameter, 0 ≤ α ≤ 1.
Original toplevel document (pdf)
cannot see any pdfsFlashcard 1332009897228
| status | not learned | measured difficulty | 37% [default] | last interval [days] | |||
|---|---|---|---|---|---|---|---|
| repetition number in this series | 0 | memorised on | scheduled repetition | ||||
| scheduled repetition interval | last repetition or drill |
Parent (intermediate) annotation
Open itA statistic is defined as a numerical quantity (such as the mean) calculated in a sample.
Original toplevel document
Subject 1. The Nature of StatisticsEstimates of these parameters taken from a sample are called statistics. Much of the field of statistics is devoted to drawing inferences from a sample concerning the value of a population parameter. <span>A statistic is defined as a numerical quantity (such as the mean) calculated in a sample. It has two different meanings. Most commonly, statistics refers to numerical data such as a company's earnings per share or average returns over the past five years. Statistics can also refer to the process of collecting, organizing, presenting, analyzing, and interpreting numerical data for the purpose of making decisions. Note that we will always know the exact composition of our sample, and by definition, we will always know the values within our sample. Ascertaining this information is the purpose of samples. Sample statistics will always be known, and can be used to estimate unknown population parameters. Hint: One way to easily remember these terms is to recall that "population" and "parameter" both start with a "p," and "sample" and "statisti
Flashcard 1332011470092
| status | not learned | measured difficulty | 37% [default] | last interval [days] | |||
|---|---|---|---|---|---|---|---|
| repetition number in this series | 0 | memorised on | scheduled repetition | ||||
| scheduled repetition interval | last repetition or drill |
Parent (intermediate) annotation
Open itA statistic is defined as a numerical quantity (such as the mean) calculated in a sample.
Original toplevel document
Subject 1. The Nature of StatisticsEstimates of these parameters taken from a sample are called statistics. Much of the field of statistics is devoted to drawing inferences from a sample concerning the value of a population parameter. <span>A statistic is defined as a numerical quantity (such as the mean) calculated in a sample. It has two different meanings. Most commonly, statistics refers to numerical data such as a company's earnings per share or average returns over the past five years. Statistics can also refer to the process of collecting, organizing, presenting, analyzing, and interpreting numerical data for the purpose of making decisions. Note that we will always know the exact composition of our sample, and by definition, we will always know the values within our sample. Ascertaining this information is the purpose of samples. Sample statistics will always be known, and can be used to estimate unknown population parameters. Hint: One way to easily remember these terms is to recall that "population" and "parameter" both start with a "p," and "sample" and "statisti
Flashcard 1332018023692
| status | not learned | measured difficulty | 37% [default] | last interval [days] | |||
|---|---|---|---|---|---|---|---|
| repetition number in this series | 0 | memorised on | scheduled repetition | ||||
| scheduled repetition interval | last repetition or drill |
Parent (intermediate) annotation
Open itthe order of the different scales is NOIR (the French word for black)
Original toplevel document
Subject 2. Measurement Scalesey. Both examples can be measured on a zero scale, where zero represents no return, or in the case of money, no money. Note that as you move down through this list, the measurement scales get stronger. <span>Hint: Remember the order of the different scales by remembering NOIR (the French word for black); the first letter of each word in the scale is indicated by the letters in the word NOIR. Before we move on, here's a quick exercise to make sure that you understand the different measurement scales. In each case, identify whether you think the data is nominal, ordinal, inter
Flashcard 1332022742284
| status | not learned | measured difficulty | 37% [default] | last interval [days] | |||
|---|---|---|---|---|---|---|---|
| repetition number in this series | 0 | memorised on | scheduled repetition | ||||
| scheduled repetition interval | last repetition or drill |
Parent (intermediate) annotation
Open itA parameter is a numerical quantity measuring some aspect of a population of scores.
Original toplevel document
Subject 1. The Nature of Statisticsve values associated with them, such as the average of all values in a sample and the average of all population values. Values from a population are called parameters, and values from a sample are called statistics. <span>A parameter is a numerical quantity measuring some aspect of a population of scores. The mean, for example, is a measure of central tendency. Greek letters are used to designate parameters. Parameters are rarely known and are usually estimated by statistics computed in samples. Populations can have many parameters, but investment analysts are usually only concerned with a few, such as the mean return or the standard deviation of returns. Estimates of these parameters taken from a sample are called statistics. Much of the field of statistics is devoted to drawing inferences from a sample concerning the value of a population parameter. A statistic is defined as a numerical quantity (such as the mean) calculated in a sample. It has two different meanings. Most commonly, statistics refers to
Flashcard 1332024315148
| status | not learned | measured difficulty | 37% [default] | last interval [days] | |||
|---|---|---|---|---|---|---|---|
| repetition number in this series | 0 | memorised on | scheduled repetition | ||||
| scheduled repetition interval | last repetition or drill |
Parent (intermediate) annotation
Open itA parameter is a numerical quantity measuring some aspect of a population of scores.
Original toplevel document
Subject 1. The Nature of Statisticsve values associated with them, such as the average of all values in a sample and the average of all population values. Values from a population are called parameters, and values from a sample are called statistics. <span>A parameter is a numerical quantity measuring some aspect of a population of scores. The mean, for example, is a measure of central tendency. Greek letters are used to designate parameters. Parameters are rarely known and are usually estimated by statistics computed in samples. Populations can have many parameters, but investment analysts are usually only concerned with a few, such as the mean return or the standard deviation of returns. Estimates of these parameters taken from a sample are called statistics. Much of the field of statistics is devoted to drawing inferences from a sample concerning the value of a population parameter. A statistic is defined as a numerical quantity (such as the mean) calculated in a sample. It has two different meanings. Most commonly, statistics refers to
Flashcard 1332040830220
| status | not learned | measured difficulty | 37% [default] | last interval [days] | |||
|---|---|---|---|---|---|---|---|
| repetition number in this series | 0 | memorised on | scheduled repetition | ||||
| scheduled repetition interval | last repetition or drill |
Parent (intermediate) annotation
Open itThe arithmetic mean is what is commonly called the average.
Original toplevel document
Subject 4. Measures of Center Tendency; The sample mean is the average for a sample. It is a statistic and is used to estimate the population mean. where n = the number of observations in the sample <span>Arithmetic Mean The arithmetic mean is what is commonly called the average. The population mean and sample mean are both examples of the arithmetic mean. If the data set encompasses an entire population, the arithmetic mean is called a population mean. If the data set includes a sample of values taken from a population, the arithmetic mean is called a sample mean. This is the most widely used measure of central tendency. When the word "mean" is used without a modifier, it can be assumed to refer to the arithmetic mean. The mean is the sum of all scores divided by the number of scores. It is used to measure the prospective (expected future) performance (return) of an investment over a number of periods. All interval and ratio data sets (e.g., incomes, ages, rates of return) have an arithmetic mean. All data values are considered and included in the arithmetic mean computation. A data set has only one arithmetic mean. This indicates that the mean is unique. The arithmetic mean is the only measure of central tendency where the sum of the deviations of each value from the mean is always zero. Deviation from the arithmetic mean is the distance between the mean and an observation in the data set. The arithmetic mean has the following disadvantages: The mean can be affected by extremes, that is, unusually large or small values. The mean cannot be determined for an open-ended data set (i.e., n is unknown). Geometric Mean The geometric mean has three important properties: It exists only if all the observations are gre
Flashcard 1332043451660
| status | not learned | measured difficulty | 37% [default] | last interval [days] | |||
|---|---|---|---|---|---|---|---|
| repetition number in this series | 0 | memorised on | scheduled repetition | ||||
| scheduled repetition interval | last repetition or drill |
Parent (intermediate) annotation
Open itThe population mean and sample mean are both examples of the arithmetic mean.
Original toplevel document
Subject 4. Measures of Center Tendency; The sample mean is the average for a sample. It is a statistic and is used to estimate the population mean. where n = the number of observations in the sample <span>Arithmetic Mean The arithmetic mean is what is commonly called the average. The population mean and sample mean are both examples of the arithmetic mean. If the data set encompasses an entire population, the arithmetic mean is called a population mean. If the data set includes a sample of values taken from a population, the arithmetic mean is called a sample mean. This is the most widely used measure of central tendency. When the word "mean" is used without a modifier, it can be assumed to refer to the arithmetic mean. The mean is the sum of all scores divided by the number of scores. It is used to measure the prospective (expected future) performance (return) of an investment over a number of periods. All interval and ratio data sets (e.g., incomes, ages, rates of return) have an arithmetic mean. All data values are considered and included in the arithmetic mean computation. A data set has only one arithmetic mean. This indicates that the mean is unique. The arithmetic mean is the only measure of central tendency where the sum of the deviations of each value from the mean is always zero. Deviation from the arithmetic mean is the distance between the mean and an observation in the data set. The arithmetic mean has the following disadvantages: The mean can be affected by extremes, that is, unusually large or small values. The mean cannot be determined for an open-ended data set (i.e., n is unknown). Geometric Mean The geometric mean has three important properties: It exists only if all the observations are gre
Flashcard 1332048432396
| status | not learned | measured difficulty | 37% [default] | last interval [days] | |||
|---|---|---|---|---|---|---|---|
| repetition number in this series | 0 | memorised on | scheduled repetition | ||||
| scheduled repetition interval | last repetition or drill |
Parent (intermediate) annotation
Open itthe arithmetic mean is the most widely used measure of central tendency.
Original toplevel document
Subject 4. Measures of Center Tendency; The sample mean is the average for a sample. It is a statistic and is used to estimate the population mean. where n = the number of observations in the sample <span>Arithmetic Mean The arithmetic mean is what is commonly called the average. The population mean and sample mean are both examples of the arithmetic mean. If the data set encompasses an entire population, the arithmetic mean is called a population mean. If the data set includes a sample of values taken from a population, the arithmetic mean is called a sample mean. This is the most widely used measure of central tendency. When the word "mean" is used without a modifier, it can be assumed to refer to the arithmetic mean. The mean is the sum of all scores divided by the number of scores. It is used to measure the prospective (expected future) performance (return) of an investment over a number of periods. All interval and ratio data sets (e.g., incomes, ages, rates of return) have an arithmetic mean. All data values are considered and included in the arithmetic mean computation. A data set has only one arithmetic mean. This indicates that the mean is unique. The arithmetic mean is the only measure of central tendency where the sum of the deviations of each value from the mean is always zero. Deviation from the arithmetic mean is the distance between the mean and an observation in the data set. The arithmetic mean has the following disadvantages: The mean can be affected by extremes, that is, unusually large or small values. The mean cannot be determined for an open-ended data set (i.e., n is unknown). Geometric Mean The geometric mean has three important properties: It exists only if all the observations are gre
Flashcard 1452417355020
| status | not learned | measured difficulty | 37% [default] | last interval [days] | |||
|---|---|---|---|---|---|---|---|
| repetition number in this series | 0 | memorised on | scheduled repetition | ||||
| scheduled repetition interval | last repetition or drill |
Parent (intermediate) annotation
Open itnalysis, we can examine whether the data are well described by the most credible possibilities in the considered set. If the data seem not to be well described, then we can consider expanding the set of possibilities. This process is called a <span>posterior predictive check<span><body><html>
Original toplevel document (pdf)
cannot see any pdfsFlashcard 1452419452172
| status | not learned | measured difficulty | 37% [default] | last interval [days] | |||
|---|---|---|---|---|---|---|---|
| repetition number in this series | 0 | memorised on | scheduled repetition | ||||
| scheduled repetition interval | last repetition or drill |
Parent (intermediate) annotation
Open ity>In general, data analysis begins with a family of candidate descriptions for the data. The descriptions are mathematical formulas that characterize the trends and spreads in the data. The formulas themselves have numbers, called parameter values, that determine the exact shape of mathematical forms.<body><html>
Original toplevel document (pdf)
cannot see any pdfsFlashcard 1452435967244
| status | not learned | measured difficulty | 37% [default] | last interval [days] | |||
|---|---|---|---|---|---|---|---|
| repetition number in this series | 0 | memorised on | scheduled repetition | ||||
| scheduled repetition interval | last repetition or drill |
Parent (intermediate) annotation
Open itThe first idea is that Bayesian inference is reallocation of credibility across possibilities.
Original toplevel document (pdf)
cannot see any pdfsFlashcard 1452437540108
| status | not learned | measured difficulty | 37% [default] | last interval [days] | |||
|---|---|---|---|---|---|---|---|
| repetition number in this series | 0 | memorised on | scheduled repetition | ||||
| scheduled repetition interval | last repetition or drill |
Parent (intermediate) annotation
Open itThe second foundational idea is that the possibilities, over which we allocate credibility, are parameter values in meaningful mathematical models.
Original toplevel document (pdf)
cannot see any pdfsFlashcard 1452439112972
| status | not learned | measured difficulty | 37% [default] | last interval [days] | |||
|---|---|---|---|---|---|---|---|
| repetition number in this series | 0 | memorised on | scheduled repetition | ||||
| scheduled repetition interval | last repetition or drill |
Parent (intermediate) annotation
Open itBecause we assume that the candidate causes are mutually exclusive and exhaust all possible causes, the total credibility across causes sums to one.
Original toplevel document (pdf)
cannot see any pdfsFlashcard 1452443045132
| status | not learned | measured difficulty | 37% [default] | last interval [days] | |||
|---|---|---|---|---|---|---|---|
| repetition number in this series | 0 | memorised on | scheduled repetition | ||||
| scheduled repetition interval | last repetition or drill |
Parent (intermediate) annotation
Open itThe distribution of credibility initially reflects prior knowledge about the possibilities, which can be quite vague. Then new data are observed, and the credibility is re-allocated. Possibilities that are consistent with the data garner more credibility, while possibilities
Original toplevel document (pdf)
cannot see any pdfsFlashcard 1452445404428
| status | not learned | measured difficulty | 37% [default] | last interval [days] | |||
|---|---|---|---|---|---|---|---|
| repetition number in this series | 0 | memorised on | scheduled repetition | ||||
| scheduled repetition interval | last repetition or drill |
Parent (intermediate) annotation
Open itYou can think of parameters as control knobs on mathematical devices that simulate data generation.
Original toplevel document (pdf)
cannot see any pdfsFlashcard 1452446977292
| status | not learned | measured difficulty | 37% [default] | last interval [days] | |||
|---|---|---|---|---|---|---|---|
| repetition number in this series | 0 | memorised on | scheduled repetition | ||||
| scheduled repetition interval | last repetition or drill |
Parent (intermediate) annotation
Open itYou can think of parameters as control knobs on mathematical devices that simulate data generation.
Original toplevel document (pdf)
cannot see any pdfsFlashcard 1452448550156
| status | not learned | measured difficulty | 37% [default] | last interval [days] | |||
|---|---|---|---|---|---|---|---|
| repetition number in this series | 0 | memorised on | scheduled repetition | ||||
| scheduled repetition interval | last repetition or drill |
Parent (intermediate) annotation
Open itThe mathematical formula for the normal distribution converts the parameter values to a particular bell-like shape for the probabilities of data values
Original toplevel document (pdf)
cannot see any pdfsFlashcard 1452450123020
| status | not learned | measured difficulty | 37% [default] | last interval [days] | |||
|---|---|---|---|---|---|---|---|
| repetition number in this series | 0 | memorised on | scheduled repetition | ||||
| scheduled repetition interval | last repetition or drill |
Parent (intermediate) annotation
Open itThe second desideratum for a mathematical description is that it should be descrip- tively adequate, which means, loosely, that the mathematical form should “look like” the data.
Original toplevel document (pdf)
cannot see any pdfsFlashcard 1452451695884
| status | not learned | measured difficulty | 37% [default] | last interval [days] | |||
|---|---|---|---|---|---|---|---|
| repetition number in this series | 0 | memorised on | scheduled repetition | ||||
| scheduled repetition interval | last repetition or drill |
Parent (intermediate) annotation
Open itThe second desideratum for a mathematical description is that it should be descrip- tively adequate, which means, loosely, that the mathematical form should “look like” the data.
Original toplevel document (pdf)
cannot see any pdfsFlashcard 1452453268748
| status | not learned | measured difficulty | 37% [default] | last interval [days] | |||
|---|---|---|---|---|---|---|---|
| repetition number in this series | 0 | memorised on | scheduled repetition | ||||
| scheduled repetition interval | last repetition or drill |
Parent (intermediate) annotation
Open itBayesian analysis is very useful for assessing the relative credibility of different candidate descriptions of data
Original toplevel document (pdf)
cannot see any pdfsFlashcard 1452454841612
| status | not learned | measured difficulty | 37% [default] | last interval [days] | |||
|---|---|---|---|---|---|---|---|
| repetition number in this series | 0 | memorised on | scheduled repetition | ||||
| scheduled repetition interval | last repetition or drill |
Parent (intermediate) annotation
Open itIn general, Bayesian analysis of data follows these steps: 1. Identify the data relevant to the research questions. What are the measurement scales of the data? Which data variables are to be predicted, and which data variables are supposed to act as predictors? 2. Define a descriptive model for the relevant data. The mathematical form and its parameters should be meaningful and appropriate to the theoretical purposes of the analysis. 3. Specif
Original toplevel document (pdf)
cannot see any pdfsFlashcard 1452457200908
| status | not learned | measured difficulty | 37% [default] | last interval [days] | |||
|---|---|---|---|---|---|---|---|
| repetition number in this series | 0 | memorised on | scheduled repetition | ||||
| scheduled repetition interval | last repetition or drill |
Parent (intermediate) annotation
Open italysis of data follows these steps: 1. Identify the data relevant to the research questions. What are the measurement scales of the data? Which data variables are to be predicted, and which data variables are supposed to act as predictors? 2. <span>Define a descriptive model for the relevant data. The mathematical form and its parameters should be meaningful and appropriate to the theoretical purposes of the analysis. 3. Specify a prior distribution on the parameters. The prior must pass muster with the audience of the analysis, such as skeptical scientists. 4. Use Bayesian inference to re-allocate c
Original toplevel document (pdf)
cannot see any pdfsFlashcard 1452459560204
| status | not learned | measured difficulty | 37% [default] | last interval [days] | |||
|---|---|---|---|---|---|---|---|
| repetition number in this series | 0 | memorised on | scheduled repetition | ||||
| scheduled repetition interval | last repetition or drill |
Parent (intermediate) annotation
Open ited, and which data variables are supposed to act as predictors? 2. Define a descriptive model for the relevant data. The mathematical form and its parameters should be meaningful and appropriate to the theoretical purposes of the analysis. 3. <span>Specify a prior distribution on the parameters. The prior must pass muster with the audience of the analysis, such as skeptical scientists. 4. Use Bayesian inference to re-allocate credibility across parameter values. Interpret the posterior distribution with respect to theoretically meaningful issues (assuming that the mod
Original toplevel document (pdf)
cannot see any pdfsFlashcard 1452461919500
| status | not learned | measured difficulty | 37% [default] | last interval [days] | |||
|---|---|---|---|---|---|---|---|
| repetition number in this series | 0 | memorised on | scheduled repetition | ||||
| scheduled repetition interval | last repetition or drill |
Parent (intermediate) annotation
Open itits parameters should be meaningful and appropriate to the theoretical purposes of the analysis. 3. Specify a prior distribution on the parameters. The prior must pass muster with the audience of the analysis, such as skeptical scientists. 4. <span>Use Bayesian inference to re-allocate credibility across parameter values. Interpret the posterior distribution with respect to theoretically meaningful issues (assuming that the model is a reasonable description of the data; see next step). 5. Check that the posterior predictions mimic the data with reasonable accuracy (i.e., conduct a “posterior predictive check”). If not, then consider a different descriptive model
Original toplevel document (pdf)
cannot see any pdfsFlashcard 1452464278796
| status | not learned | measured difficulty | 37% [default] | last interval [days] | |||
|---|---|---|---|---|---|---|---|
| repetition number in this series | 0 | memorised on | scheduled repetition | ||||
| scheduled repetition interval | last repetition or drill |
Parent (intermediate) annotation
Open ite Bayesian inference to re-allocate credibility across parameter values. Interpret the posterior distribution with respect to theoretically meaningful issues (assuming that the model is a reasonable description of the data; see next step). 5. <span>Check that the posterior predictions mimic the data with reasonable accuracy (i.e., conduct a “posterior predictive check”). If not, then consider a different descriptive model<span><body><html>
Original toplevel document (pdf)
cannot see any pdfsFlashcard 1452472929548
| status | not learned | measured difficulty | 37% [default] | last interval [days] | |||
|---|---|---|---|---|---|---|---|
| repetition number in this series | 0 | memorised on | scheduled repetition | ||||
| scheduled repetition interval | last repetition or drill |
Parent (intermediate) annotation
Open itOne way to summarize the uncertainty is by marking the span of values that are most credible and cover 95% of the distribution. This is called the highest density inter val (HDI) and is marked by the black bar on the floor of the distribution in Figure 2.5.
Original toplevel document (pdf)
cannot see any pdfsFlashcard 1452686576908
| status | not learned | measured difficulty | 37% [default] | last interval [days] | |||
|---|---|---|---|---|---|---|---|
| repetition number in this series | 0 | memorised on | scheduled repetition | ||||
| scheduled repetition interval | last repetition or drill |
Parent (intermediate) annotation
Open itBayesian analysis re- allocates credibility among parameter values within a meaningful space of possibilities defined by the chosen model.
Original toplevel document (pdf)
cannot see any pdfsFlashcard 1455233305868
| status | not learned | measured difficulty | 37% [default] | last interval [days] | |||
|---|---|---|---|---|---|---|---|
| repetition number in this series | 0 | memorised on | scheduled repetition | ||||
| scheduled repetition interval | last repetition or drill |
Parent (intermediate) annotation
Open itThe standard deviation is another control knob in the mathematical formula for the normal distribution that controls the width or dispersion of the distribution. The standard deviation is sometimes called a scale parameter.
Original toplevel document (pdf)
cannot see any pdfsFlashcard 1455255325964
| status | not learned | measured difficulty | 37% [default] | last interval [days] | |||
|---|---|---|---|---|---|---|---|
| repetition number in this series | 0 | memorised on | scheduled repetition | ||||
| scheduled repetition interval | last repetition or drill |
Parent (intermediate) annotation
Open ito make inferences from data without using a model is a method from NHST called resampling or bootstrapping. These methods compute p values to make decisions, and p values have fundamental logical problems that will be discussed in Chapter 11. <span>These methods also have very limited ability to express degrees of certainty about characteristics of the data, whereas Bayesian methods put expression of uncertainty front and center<span><body><html>
Original toplevel document (pdf)
cannot see any pdfsFlashcard 1456514141452
| status | not learned | measured difficulty | 37% [default] | last interval [days] | |||
|---|---|---|---|---|---|---|---|
| repetition number in this series | 0 | memorised on | scheduled repetition | ||||
| scheduled repetition interval | last repetition or drill |
Parent (intermediate) annotation
Open itThe mean is a control knob in the mathematical formula for the normal distribution that controls the location of the distribution’s central tendency. The mean is sometimes called a location parameter.
Original toplevel document (pdf)
cannot see any pdfsFlashcard 1456515714316
| status | not learned | measured difficulty | 37% [default] | last interval [days] | |||
|---|---|---|---|---|---|---|---|
| repetition number in this series | 0 | memorised on | scheduled repetition | ||||
| scheduled repetition interval | last repetition or drill |
Parent (intermediate) annotation
Open itThe mean is a control knob in the mathematical formula for the normal distribution that controls the location of the distribution’s central tendency. The mean is sometimes called a location parameter.
Original toplevel document (pdf)
cannot see any pdfsFlashcard 1457076440332
| status | not learned | measured difficulty | 37% [default] | last interval [days] | |||
|---|---|---|---|---|---|---|---|
| repetition number in this series | 0 | memorised on | scheduled repetition | ||||
| scheduled repetition interval | last repetition or drill |
Parent (intermediate) annotation
Open itA matrix is simply a two-dimensional array of values of the same type.
Original toplevel document (pdf)
cannot see any pdfsFlashcard 1457142500620
| status | not learned | measured difficulty | 37% [default] | last interval [days] | |||
|---|---|---|---|---|---|---|---|
| repetition number in this series | 0 | memorised on | scheduled repetition | ||||
| scheduled repetition interval | last repetition or drill |
Parent (intermediate) annotation
Open itWhenever we ask about how likely an outcome is, we always ask with a set of possible outcomes in mind. This set exhausts all possible outcomes, and the outcomes are all mutually exclusive. This set is called the sample space
Original toplevel document (pdf)
cannot see any pdfsFlashcard 1457144859916
| status | not learned | measured difficulty | 37% [default] | last interval [days] | |||
|---|---|---|---|---|---|---|---|
| repetition number in this series | 0 | memorised on | scheduled repetition | ||||
| scheduled repetition interval | last repetition or drill |
Parent (intermediate) annotation
Open itMany coins minted by governments have the picture of an important person’s head on one side. This side is called “heads” or, technically, the “obverse.”
Original toplevel document (pdf)
cannot see any pdfsFlashcard 1457186540812
| status | not learned | measured difficulty | 37% [default] | last interval [days] | |||
|---|---|---|---|---|---|---|---|
| repetition number in this series | 0 | memorised on | scheduled repetition | ||||
| scheduled repetition interval | last repetition or drill |
Parent (intermediate) annotation
Open itAn array is a generalization of a matrix to multiple dimensions
Original toplevel document (pdf)
cannot see any pdfsFlashcard 1457245785356
| status | not learned | measured difficulty | 37% [default] | last interval [days] | |||
|---|---|---|---|---|---|---|---|
| repetition number in this series | 0 | memorised on | scheduled repetition | ||||
| scheduled repetition interval | last repetition or drill |
Parent (intermediate) annotation
Open itOne case of trying to make inferences from data without using a model is a method from NHST called resampling or bootstrapping.
Original toplevel document (pdf)
cannot see any pdfsFlashcard 1471357259020
| status | not learned | measured difficulty | 37% [default] | last interval [days] | |||
|---|---|---|---|---|---|---|---|
| repetition number in this series | 0 | memorised on | scheduled repetition | ||||
| scheduled repetition interval | last repetition or drill |
Parent (intermediate) annotation
Open itIn general, a probability, whether it’s outside the head or inside the head, is just a way of assigning numbers to a set of mutually exclusive possibilities
Original toplevel document (pdf)
cannot see any pdfsFlashcard 1471358831884
| status | not learned | measured difficulty | 37% [default] | last interval [days] | |||
|---|---|---|---|---|---|---|---|
| repetition number in this series | 0 | memorised on | scheduled repetition | ||||
| scheduled repetition interval | last repetition or drill |
Parent (intermediate) annotation
Open itA probability distribution is simply a list of all possible outcomes and their corresponding probabilities
Original toplevel document (pdf)
cannot see any pdfsFlashcard 1471421746444
| status | not learned | measured difficulty | 37% [default] | last interval [days] | |||
|---|---|---|---|---|---|---|---|
| repetition number in this series | 0 | memorised on | scheduled repetition | ||||
| scheduled repetition interval | last repetition or drill |
Parent (intermediate) annotation
Open itFor continuous outcome spaces, we can discretize the space into a finite set of mutually exclusive and exhaustive “bins.”
Original toplevel document (pdf)
cannot see any pdfsFlashcard 1471423319308
| status | not learned | measured difficulty | 37% [default] | last interval [days] | |||
|---|---|---|---|---|---|---|---|
| repetition number in this series | 0 | memorised on | scheduled repetition | ||||
| scheduled repetition interval | last repetition or drill |
Parent (intermediate) annotation
Open itLoosely speaking, the term “mass” refers the amount of stuff in an object. When the stuff is probability and the object is an interval of a scale, then the mass is the proportion of the outcomes in the interval.
Original toplevel document (pdf)
cannot see any pdfsFlashcard 1471424892172
| status | not learned | measured difficulty | 37% [default] | last interval [days] | |||
|---|---|---|---|---|---|---|---|
| repetition number in this series | 0 | memorised on | scheduled repetition | ||||
| scheduled repetition interval | last repetition or drill |
Parent (intermediate) annotation
Open itThe problem with using intervals, however, is that their widths and edges are arbitrary, and wide intervals are not very precise. Therefore, what we will do is make the intervals infinitesimally narrow, and instead of talking about the infinitesimal probability mass of each infinitesimal interval, we will talk ab
Original toplevel document (pdf)
cannot see any pdfsFlashcard 1471428037900
| status | not learned | measured difficulty | 37% [default] | last interval [days] | |||
|---|---|---|---|---|---|---|---|
| repetition number in this series | 0 | memorised on | scheduled repetition | ||||
| scheduled repetition interval | last repetition or drill |
Parent (intermediate) annotation
Open itand wide intervals are not very precise. Therefore, what we will do is make the intervals infinitesimally narrow, and instead of talking about the infinitesimal probability mass of each infinitesimal interval, we will talk about the ratio of <span>the probability mass to the interval width. That ratio is called the probability density.<span><body><html>
Original toplevel document (pdf)
cannot see any pdfsFlashcard 1471429610764
| status | not learned | measured difficulty | 37% [default] | last interval [days] | |||
|---|---|---|---|---|---|---|---|
| repetition number in this series | 0 | memorised on | scheduled repetition | ||||
| scheduled repetition interval | last repetition or drill |
Parent (intermediate) annotation
Open iterefore, what we will do is make the intervals infinitesimally narrow, and instead of talking about the infinitesimal probability mass of each infinitesimal interval, we will talk about the ratio of the probability mass to the interval width. <span>That ratio is called the probability density.<span><body><html>
Original toplevel document (pdf)
cannot see any pdfsFlashcard 1471506681100
| status | not learned | measured difficulty | 37% [default] | last interval [days] | |||
|---|---|---|---|---|---|---|---|
| repetition number in this series | 0 | memorised on | scheduled repetition | ||||
| scheduled repetition interval | last repetition or drill |
Parent (intermediate) annotation
Open itYour job in answering that question is to provide a number between 0 and 1 that accurately reflects your belief probability. One way to come up with such a number is to calibrate your beliefs relative to other events with clear probabilities
Original toplevel document (pdf)
cannot see any pdfsFlashcard 1471508253964
| status | not learned | measured difficulty | 37% [default] | last interval [days] | |||
|---|---|---|---|---|---|---|---|
| repetition number in this series | 0 | memorised on | scheduled repetition | ||||
| scheduled repetition interval | last repetition or drill |
Parent (intermediate) annotation
Open itThe probability of a discrete outcome, such as the probability of falling into an interval on a continuous scale, is referred to as a probability mass
Original toplevel document (pdf)
cannot see any pdfsFlashcard 1641142947084
| status | not learned | measured difficulty | 37% [default] | last interval [days] | |||
|---|---|---|---|---|---|---|---|
| repetition number in this series | 0 | memorised on | scheduled repetition | ||||
| scheduled repetition interval | last repetition or drill |
Parent (intermediate) annotation
Open itHarmonic Mean The harmonic mean of n numbers x i (where i = 1, 2, ..., n) is: The special cases of n = 2 and n = 3 are given by: and so on.
Original toplevel document
Subject 4. Measures of Center Tendency, therefore, is not recommended for use as the only measure of central tendency. A further disadvantage of the mode is that many distributions have more than one mode. These distributions are called "multimodal." <span>Harmonic Mean The harmonic mean of n numbers x i (where i = 1, 2, ..., n) is: The special cases of n = 2 and n = 3 are given by: and so on. For n = 2, the harmonic mean is related to arithmetic mean A and geometric mean G by: The mean, median, and mode are equal in symmetric distributions. The mean is higher than the median in positively skewed distributions and lower than the median in negatively skewed dist
Flashcard 1641160772876
| status | not learned | measured difficulty | 37% [default] | last interval [days] | |||
|---|---|---|---|---|---|---|---|
| repetition number in this series | 0 | memorised on | scheduled repetition | ||||
| scheduled repetition interval | last repetition or drill |
Parent (intermediate) annotation
Open itrs x i (where i = 1, 2, ..., n) is: The special cases of n = 2 and n = 3 are given by: and so on. <span>For n = 2, the harmonic mean is related to arithmetic mean A and geometric mean G by: <span><body><html>
Original toplevel document
Subject 4. Measures of Center Tendency, therefore, is not recommended for use as the only measure of central tendency. A further disadvantage of the mode is that many distributions have more than one mode. These distributions are called "multimodal." <span>Harmonic Mean The harmonic mean of n numbers x i (where i = 1, 2, ..., n) is: The special cases of n = 2 and n = 3 are given by: and so on. For n = 2, the harmonic mean is related to arithmetic mean A and geometric mean G by: The mean, median, and mode are equal in symmetric distributions. The mean is higher than the median in positively skewed distributions and lower than the median in negatively skewed dist
Flashcard 1641163132172
| status | not learned | measured difficulty | 37% [default] | last interval [days] | |||
|---|---|---|---|---|---|---|---|
| repetition number in this series | 0 | memorised on | scheduled repetition | ||||
| scheduled repetition interval | last repetition or drill |
Parent (intermediate) annotation
Open itHarmonic Mean The harmonic mean of n numbers x i (where i = 1, 2, ..., n) is: The special cases of n = 2 and n = 3 are given by: and so on. For n = 2, the harmonic mean is related to arithmetic mean A and geometric mea
Original toplevel document
Subject 4. Measures of Center Tendency, therefore, is not recommended for use as the only measure of central tendency. A further disadvantage of the mode is that many distributions have more than one mode. These distributions are called "multimodal." <span>Harmonic Mean The harmonic mean of n numbers x i (where i = 1, 2, ..., n) is: The special cases of n = 2 and n = 3 are given by: and so on. For n = 2, the harmonic mean is related to arithmetic mean A and geometric mean G by: The mean, median, and mode are equal in symmetric distributions. The mean is higher than the median in positively skewed distributions and lower than the median in negatively skewed dist
Flashcard 1641164705036
| status | not learned | measured difficulty | 37% [default] | last interval [days] | |||
|---|---|---|---|---|---|---|---|
| repetition number in this series | 0 | memorised on | scheduled repetition | ||||
| scheduled repetition interval | last repetition or drill |
Parent (intermediate) annotation
Open itHarmonic Mean The harmonic mean of n numbers x i (where i = 1, 2, ..., n) is: The special cases of n = 2 and n = 3 are given by: and so on. For n = 2, the harmonic mean is related to arithmetic mean A and geometric mea
Original toplevel document
Subject 4. Measures of Center Tendency, therefore, is not recommended for use as the only measure of central tendency. A further disadvantage of the mode is that many distributions have more than one mode. These distributions are called "multimodal." <span>Harmonic Mean The harmonic mean of n numbers x i (where i = 1, 2, ..., n) is: The special cases of n = 2 and n = 3 are given by: and so on. For n = 2, the harmonic mean is related to arithmetic mean A and geometric mean G by: The mean, median, and mode are equal in symmetric distributions. The mean is higher than the median in positively skewed distributions and lower than the median in negatively skewed dist
Flashcard 1645014551820
| status | not learned | measured difficulty | 37% [default] | last interval [days] | |||
|---|---|---|---|---|---|---|---|
| repetition number in this series | 0 | memorised on | scheduled repetition | ||||
| scheduled repetition interval | last repetition or drill |
Parent (intermediate) annotation
Open itHarmonic Mean The harmonic mean of n numbers x i (where i = 1, 2, ..., n) is: The special cases of n = 2 and n = 3 are given by: and so on.
Original toplevel document
Subject 4. Measures of Center Tendency, therefore, is not recommended for use as the only measure of central tendency. A further disadvantage of the mode is that many distributions have more than one mode. These distributions are called "multimodal." <span>Harmonic Mean The harmonic mean of n numbers x i (where i = 1, 2, ..., n) is: The special cases of n = 2 and n = 3 are given by: and so on. For n = 2, the harmonic mean is related to arithmetic mean A and geometric mean G by: The mean, median, and mode are equal in symmetric distributions. The mean is higher than the median in positively skewed distributions and lower than the median in negatively skewed dist
Flashcard 1645933628684
| status | not learned | measured difficulty | 37% [default] | last interval [days] | |||
|---|---|---|---|---|---|---|---|
| repetition number in this series | 0 | memorised on | scheduled repetition | ||||
| scheduled repetition interval | last repetition or drill |
Flashcard 3111646792972
| status | not learned | measured difficulty | 37% [default] | last interval [days] | |||
|---|---|---|---|---|---|---|---|
| repetition number in this series | 0 | memorised on | scheduled repetition | ||||
| scheduled repetition interval | last repetition or drill |
Flashcard 3111649152268
| status | not learned | measured difficulty | 37% [default] | last interval [days] | |||
|---|---|---|---|---|---|---|---|
| repetition number in this series | 0 | memorised on | scheduled repetition | ||||
| scheduled repetition interval | last repetition or drill |
Flashcard 3111650987276
| status | not learned | measured difficulty | 37% [default] | last interval [days] | |||
|---|---|---|---|---|---|---|---|
| repetition number in this series | 0 | memorised on | scheduled repetition | ||||
| scheduled repetition interval | last repetition or drill |
Flashcard 3126364605708
| status | not learned | measured difficulty | 37% [default] | last interval [days] | |||
|---|---|---|---|---|---|---|---|
| repetition number in this series | 0 | memorised on | scheduled repetition | ||||
| scheduled repetition interval | last repetition or drill |
Flashcard 3126366440716
| status | not learned | measured difficulty | 37% [default] | last interval [days] | |||
|---|---|---|---|---|---|---|---|
| repetition number in this series | 0 | memorised on | scheduled repetition | ||||
| scheduled repetition interval | last repetition or drill |
Flashcard 3963046464780
| status | not learned | measured difficulty | 37% [default] | last interval [days] | |||
|---|---|---|---|---|---|---|---|
| repetition number in this series | 0 | memorised on | scheduled repetition | ||||
| scheduled repetition interval | last repetition or drill |
Flashcard 4009031765260
| status | not learned | measured difficulty | 37% [default] | last interval [days] | |||
|---|---|---|---|---|---|---|---|
| repetition number in this series | 0 | memorised on | scheduled repetition | ||||
| scheduled repetition interval | last repetition or drill |
Flashcard 4028512472332
| status | not learned | measured difficulty | 37% [default] | last interval [days] | |||
|---|---|---|---|---|---|---|---|
| repetition number in this series | 0 | memorised on | scheduled repetition | ||||
| scheduled repetition interval | last repetition or drill |
Flashcard 4028517977356
| status | not learned | measured difficulty | 37% [default] | last interval [days] | |||
|---|---|---|---|---|---|---|---|
| repetition number in this series | 0 | memorised on | scheduled repetition | ||||
| scheduled repetition interval | last repetition or drill |
Flashcard 4344775576844
| status | not learned | measured difficulty | 37% [default] | last interval [days] | |||
|---|---|---|---|---|---|---|---|
| repetition number in this series | 0 | memorised on | scheduled repetition | ||||
| scheduled repetition interval | last repetition or drill |
Parent (intermediate) annotation
Open itWhen you pass a tuple as the first argument in an assert statement, the assertion always evaluates as true and therefore never fails.
Original toplevel document
Assert Statements in Python – dbader.orgvaluate to true. I’ve been bitten by this myself in the past. I wrote a longer article about this specific issue you can check out by clicking here. Alternatively, here’s the executive summary: <span>When you pass a tuple as the first argument in an assert statement, the assertion always evaluates as true and therefore never fails. For example, this assertion will never fail: assert(1 == 2, 'This should fail') This has to do with non-empty tuples always being truthy in Python. If you pass a tuple to an assert stat
Flashcard 4344779509004
| status | not learned | measured difficulty | 37% [default] | last interval [days] | |||
|---|---|---|---|---|---|---|---|
| repetition number in this series | 0 | memorised on | scheduled repetition | ||||
| scheduled repetition interval | last repetition or drill |
Parent (intermediate) annotation
Open itWhen you pass a tuple as the first argument in an assert statement, the assertion always evaluates as true and therefore never fails.
Original toplevel document
Assert Statements in Python – dbader.orgvaluate to true. I’ve been bitten by this myself in the past. I wrote a longer article about this specific issue you can check out by clicking here. Alternatively, here’s the executive summary: <span>When you pass a tuple as the first argument in an assert statement, the assertion always evaluates as true and therefore never fails. For example, this assertion will never fail: assert(1 == 2, 'This should fail') This has to do with non-empty tuples always being truthy in Python. If you pass a tuple to an assert stat
| status | not read | reprioritisations | ||
|---|---|---|---|---|
| last reprioritisation on | suggested re-reading day | |||
| started reading on | finished reading on |
Сновидение — Википедия
идений 2.1 По З. Фрейду 2.2 Толкование сновидений К. Юнга 3 «Управление» сновидениями 4 Сновидение в религии 5 Дежавю 6 См. также 7 Примечания 8 Литература Общие сведения[править | править код] <span>Наука, изучающая сон, называется сомнология, сновидения — онейрология. Сновидения считаются связанными с фазой быстрого движения глаз (БДГ). Эта стадия возникает примерно каждые 1,5—2 часа сна, и её продолжительность постепенно удлиняется. Она характеризуе
Flashcard 4345012030732
| status | not learned | measured difficulty | 37% [default] | last interval [days] | |||
|---|---|---|---|---|---|---|---|
| repetition number in this series | 0 | memorised on | scheduled repetition | ||||
| scheduled repetition interval | last repetition or drill |
Parent (intermediate) annotation
Open itНаука, изучающая сон , называется сомнология , сновидения — онейрология .
Original toplevel document
Сновидение — Википедияидений 2.1 По З. Фрейду 2.2 Толкование сновидений К. Юнга 3 «Управление» сновидениями 4 Сновидение в религии 5 Дежавю 6 См. также 7 Примечания 8 Литература Общие сведения[править | править код] <span>Наука, изучающая сон, называется сомнология, сновидения — онейрология. Сновидения считаются связанными с фазой быстрого движения глаз (БДГ). Эта стадия возникает примерно каждые 1,5—2 часа сна, и её продолжительность постепенно удлиняется. Она характеризуе
Flashcard 4345013603596
| status | not learned | measured difficulty | 37% [default] | last interval [days] | |||
|---|---|---|---|---|---|---|---|
| repetition number in this series | 0 | memorised on | scheduled repetition | ||||
| scheduled repetition interval | last repetition or drill |
Parent (intermediate) annotation
Open itНаука, изучающая сон , называется сомнология , сновидения — онейрология .
Original toplevel document
Сновидение — Википедияидений 2.1 По З. Фрейду 2.2 Толкование сновидений К. Юнга 3 «Управление» сновидениями 4 Сновидение в религии 5 Дежавю 6 См. также 7 Примечания 8 Литература Общие сведения[править | править код] <span>Наука, изучающая сон, называется сомнология, сновидения — онейрология. Сновидения считаются связанными с фазой быстрого движения глаз (БДГ). Эта стадия возникает примерно каждые 1,5—2 часа сна, и её продолжительность постепенно удлиняется. Она характеризуе
| status | not read | reprioritisations | ||
|---|---|---|---|---|
| last reprioritisation on | suggested re-reading day | |||
| started reading on | finished reading on |