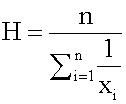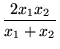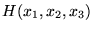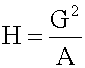Edited, memorised or added to reading queue
on 19-Jul-2017 (Wed)
Do you want BuboFlash to help you learning these things? Click here to log in or create user.
Flashcard 1429113539852
| status | not learned | measured difficulty | 37% [default] | last interval [days] | |||
|---|---|---|---|---|---|---|---|
| repetition number in this series | 0 | memorised on | scheduled repetition | ||||
| scheduled repetition interval | last repetition or drill |
Parent (intermediate) annotation
Open itEffectiveness is the norm of rhetoric.
Original toplevel document (pdf)
cannot see any pdfsFlashcard 1432865082636
| status | not learned | measured difficulty | 37% [default] | last interval [days] | |||
|---|---|---|---|---|---|---|---|
| repetition number in this series | 0 | memorised on | scheduled repetition | ||||
| scheduled repetition interval | last repetition or drill |
Parent (intermediate) annotation
Open itMusical=rhythmic, e.g. music performance, singing, musical composition, rhythmic patterns.
Original toplevel document (pdf)
cannot see any pdfsFlashcard 1433034689804
| status | not learned | measured difficulty | 37% [default] | last interval [days] | |||
|---|---|---|---|---|---|---|---|
| repetition number in this series | 0 | memorised on | scheduled repetition | ||||
| scheduled repetition interval | last repetition or drill |
Parent (intermediate) annotation
Open itVerbs normally have two voices: active and passive.
Original toplevel document (pdf)
cannot see any pdfsFlashcard 1610314288396
| status | not learned | measured difficulty | 37% [default] | last interval [days] | |||
|---|---|---|---|---|---|---|---|
| repetition number in this series | 0 | memorised on | scheduled repetition | ||||
| scheduled repetition interval | last repetition or drill |
Flashcard 1621283179788
| status | not learned | measured difficulty | 37% [default] | last interval [days] | |||
|---|---|---|---|---|---|---|---|
| repetition number in this series | 0 | memorised on | scheduled repetition | ||||
| scheduled repetition interval | last repetition or drill |
Subject 3. Cash Flow Statement Analysis
; Free cash flow = CFO - capital expenditure Free Cash Flow to the Firm (FCFF): Cash available to shareholders and bondholders after taxes, capital investment, and WC investment. <span>FCFF = NI + NCC + Int (1 - Tax rate) - FCInv - WCInv NI: Net income available to common shareholders. It is the company's earnings after interest, taxes and preferred dividends. NCC: Net non-cash
Flashcard 1635085585676
| status | not learned | measured difficulty | 37% [default] | last interval [days] | |||
|---|---|---|---|---|---|---|---|
| repetition number in this series | 0 | memorised on | scheduled repetition | ||||
| scheduled repetition interval | last repetition or drill |
Open it
where the returns are centered (central tendency); how far returns are dispersed from their center (dispersion); whether the distribution of returns is symmetrically shaped or lopsided (skewness); and whether extreme outcomes are likely (kurtosis).
Flashcard 1636237184268
| status | not learned | measured difficulty | 37% [default] | last interval [days] | |||
|---|---|---|---|---|---|---|---|
| repetition number in this series | 0 | memorised on | scheduled repetition | ||||
| scheduled repetition interval | last repetition or drill |
Subject 3. Frequency Distributions
ency distribution. An interval, also called a class, is a set of values within which an observation falls. Each interval has a lower limit and an upper limit. Intervals must be all-inclusive and non-overlapping. <span>A frequency distribution is a tabular display of data categorized into a small number of non-overlapping intervals. Note that: Each observation can only lie in one interval. The total number of intervals will incorporate the whole population. The range for an interval is unique. This mean
| status | not read | reprioritisations | ||
|---|---|---|---|---|
| last reprioritisation on | suggested re-reading day | |||
| started reading on | finished reading on |
Subject 3. Frequency Distributions
that: Each observation can only lie in one interval. The total number of intervals will incorporate the whole population. The range for an interval is unique. This means a value (observation) can only fall into one interval. <span>It is important to consider the number of intervals to be used. If too few intervals are used, too much data may be summarized and we may lose important characteristics; if too many intervals are used, we may not summarize enough. A frequency distribution is constructed by dividing the scores into intervals and counting the number of scores in each interval. The actual number of scores and the percent
Flashcard 1636479143180
| status | not learned | measured difficulty | 37% [default] | last interval [days] | |||
|---|---|---|---|---|---|---|---|
| repetition number in this series | 0 | memorised on | scheduled repetition | ||||
| scheduled repetition interval | last repetition or drill |
Subject 3. Frequency Distributions
the heights of bars drawn next to each other). The classes (intervals) are shown on the horizontal (x) axis. There is no space between the bars. From a histogram, we can see quickly where most of the observations lie. <span>The shapes of histograms will vary, depending on the choice of the size of the intervals. 2. The frequency polygon is another means of graphically displaying data. It is similar to a histogram but the bars are replaced by a line joined together. It is constructe
Flashcard 1636489366796
| status | not learned | measured difficulty | 37% [default] | last interval [days] | |||
|---|---|---|---|---|---|---|---|
| repetition number in this series | 0 | memorised on | scheduled repetition | ||||
| scheduled repetition interval | last repetition or drill |
Subject 3. Frequency Distributions
first to draw a histogram in pencil, then to plot the points and join the lines, and finally to rub out the histogram. In this way, the histogram can be used as an initial guide to drawing the polygon. <span>The relative frequency for a class is calculated by dividing the number of observations in a class by the total number of observations and converting this figure to a percentage (multiplying the fraction by 100). Simply, relative frequency is the percentage of total observations falling within each interval. It is another way of analyzing data; it tells us, for each class, what proportion (or pe
Flashcard 1636579020044
| status | not learned | measured difficulty | 37% [default] | last interval [days] | |||
|---|---|---|---|---|---|---|---|
| repetition number in this series | 0 | memorised on | scheduled repetition | ||||
| scheduled repetition interval | last repetition or drill |
Subject 4. Measures of Center Tendency
value that stands in the middle of the data set, and divides it into two equal halves, with an equal number of data values in each half. To determine the median, arrange the data from highest to lowest (or lowest to highest) and <span>find the middle observation. If there are an odd number of observations in the data set, the median is the middle observation (n + 1)/2 of the data set. If the number of observations is even, there is no single mid
Flashcard 1636598680844
| status | not learned | measured difficulty | 37% [default] | last interval [days] | |||
|---|---|---|---|---|---|---|---|
| repetition number in this series | 0 | memorised on | scheduled repetition | ||||
| scheduled repetition interval | last repetition or drill |
Google Übersetzer
referably outside. Automatisch von Google übersetzt Ideally you would practice it in the sun, preferably outside or in a sunny room. Automatisch von Google übersetzt 13 weitere Beispiele Siehe auch lieber mögen, lieber haben Übersetzungen für <span>preferably Adverb vorzugsweise preferably, mainly, chiefly möglichst preferably besser better, preferably lieber rather, better, preferably, sooner Google Übersetzer für Unternehmen:Translator Too
referably outside. Automatisch von Google übersetzt Ideally you would practice it in the sun, preferably outside or in a sunny room. Automatisch von Google übersetzt 13 weitere Beispiele Siehe auch lieber mögen, lieber haben Übersetzungen für <span>preferably Adverb vorzugsweise preferably, mainly, chiefly möglichst preferably besser better, preferably lieber rather, better, preferably, sooner Google Übersetzer für Unternehmen:Translator Too
Flashcard 1636600777996
| status | not learned | measured difficulty | 37% [default] | last interval [days] | |||
|---|---|---|---|---|---|---|---|
| repetition number in this series | 0 | memorised on | scheduled repetition | ||||
| scheduled repetition interval | last repetition or drill |
Google Übersetzer
omatisch von Google übersetzt The session should be as short and as intensive as possible, preferably two or three days. Automatisch von Google übersetzt 13 weitere Beispiele Siehe auch lieber mögen, lieber haben Übersetzungen für preferably <span>Adverb vorzugsweise preferably, mainly, chiefly möglichst preferably besser better, preferably lieber rather, better, preferably, sooner Google Übersetzer für Unternehmen:Translator ToolkitWebsite-Übersetzer Ziehe die Datei oder den Link auf diesen Bereich, um das Dokument oder die Webseite zu übersetzen. Ziehe den Lin
omatisch von Google übersetzt The session should be as short and as intensive as possible, preferably two or three days. Automatisch von Google übersetzt 13 weitere Beispiele Siehe auch lieber mögen, lieber haben Übersetzungen für preferably <span>Adverb vorzugsweise preferably, mainly, chiefly möglichst preferably besser better, preferably lieber rather, better, preferably, sooner Google Übersetzer für Unternehmen:Translator ToolkitWebsite-Übersetzer Ziehe die Datei oder den Link auf diesen Bereich, um das Dokument oder die Webseite zu übersetzen. Ziehe den Lin
| status | not read | reprioritisations | ||
|---|---|---|---|---|
| last reprioritisation on | suggested re-reading day | |||
| started reading on | finished reading on |
| status | not read | reprioritisations | ||
|---|---|---|---|---|
| last reprioritisation on | suggested re-reading day | |||
| started reading on | finished reading on |
| status | not read | reprioritisations | ||
|---|---|---|---|---|
| last reprioritisation on | suggested re-reading day | |||
| started reading on | finished reading on |
| status | not read | reprioritisations | ||
|---|---|---|---|---|
| last reprioritisation on | suggested re-reading day | |||
| started reading on | finished reading on |
| status | not read | reprioritisations | ||
|---|---|---|---|---|
| last reprioritisation on | suggested re-reading day | |||
| started reading on | finished reading on |
Flashcard 1636617817356
| status | not learned | measured difficulty | 37% [default] | last interval [days] | |||
|---|---|---|---|---|---|---|---|
| repetition number in this series | 0 | memorised on | scheduled repetition | ||||
| scheduled repetition interval | last repetition or drill |
Subject 4. Measures of Center Tendency
dle of the data set, and divides it into two equal halves, with an equal number of data values in each half. To determine the median, arrange the data from highest to lowest (or lowest to highest) and find the middle observation. <span>If there are an odd number of observations in the data set, the median is the middle observation (n + 1)/2 of the data set. If the number of observations is even, there is no single middle observation (there are two, actually). To find the median, take the arithmetic mean of the two middle o
Flashcard 1636620963084
| status | not learned | measured difficulty | 37% [default] | last interval [days] | |||
|---|---|---|---|---|---|---|---|
| repetition number in this series | 0 | memorised on | scheduled repetition | ||||
| scheduled repetition interval | last repetition or drill |
Subject 4. Measures of Center Tendency
determine the median, arrange the data from highest to lowest (or lowest to highest) and find the middle observation. If there are an odd number of observations in the data set, the median is the middle observation (n + 1)/2 of the data set. <span>If the number of observations is even, there is no single middle observation (there are two, actually). To find the median, take the arithmetic mean of the two middle observations. The median is less sensitive to extreme scores than the mean. This makes it a better measure than the mean for highly skewed distributions. Looking at median income is usua
Flashcard 1636623322380
| status | not learned | measured difficulty | 37% [default] | last interval [days] | |||
|---|---|---|---|---|---|---|---|
| repetition number in this series | 0 | memorised on | scheduled repetition | ||||
| scheduled repetition interval | last repetition or drill |
Subject 4. Measures of Center Tendency
he middle observation (n + 1)/2 of the data set. If the number of observations is even, there is no single middle observation (there are two, actually). To find the median, take the arithmetic mean of the two middle observations. <span>The median is less sensitive to extreme scores than the mean. This makes it a better measure than the mean for highly skewed distributions. Looking at median income is usually more informative than looking at mean income, for example. The sum of the absolute deviations of each number from the median is lower than the sum of
Flashcard 1636625681676
| status | not learned | measured difficulty | 37% [default] | last interval [days] | |||
|---|---|---|---|---|---|---|---|
| repetition number in this series | 0 | memorised on | scheduled repetition | ||||
| scheduled repetition interval | last repetition or drill |
Subject 4. Measures of Center Tendency
, actually). To find the median, take the arithmetic mean of the two middle observations. The median is less sensitive to extreme scores than the mean. This makes it a better measure than the mean for highly skewed distributions. <span>Looking at median income is usually more informative than looking at mean income, for example. The sum of the absolute deviations of each number from the median is lower than the sum of absolute deviations from any other number. Note that whenever you c
Flashcard 1636628040972
| status | not learned | measured difficulty | 37% [default] | last interval [days] | |||
|---|---|---|---|---|---|---|---|
| repetition number in this series | 0 | memorised on | scheduled repetition | ||||
| scheduled repetition interval | last repetition or drill |
Subject 4. Measures of Center Tendency
The median is less sensitive to extreme scores than the mean. This makes it a better measure than the mean for highly skewed distributions. Looking at median income is usually more informative than looking at mean income, for example. <span>The sum of the absolute deviations of each number from the median is lower than the sum of absolute deviations from any other number. Note that whenever you calculate a median, it is imperative that you place the data in order first. It does not matter whether you order the data from smallest to largest o
Flashcard 1636630400268
| status | not learned | measured difficulty | 37% [default] | last interval [days] | |||
|---|---|---|---|---|---|---|---|
| repetition number in this series | 0 | memorised on | scheduled repetition | ||||
| scheduled repetition interval | last repetition or drill |
Subject 4. Measures of Center Tendency
t median income is usually more informative than looking at mean income, for example. The sum of the absolute deviations of each number from the median is lower than the sum of absolute deviations from any other number. Note that <span>whenever you calculate a median, it is imperative that you place the data in order first. It does not matter whether you order the data from smallest to largest or from largest to smallest, but it does matter that you order the data. Mode Mode means
Flashcard 1636632759564
| status | not learned | measured difficulty | 37% [default] | last interval [days] | |||
|---|---|---|---|---|---|---|---|
| repetition number in this series | 0 | memorised on | scheduled repetition | ||||
| scheduled repetition interval | last repetition or drill |
Subject 4. Measures of Center Tendency
a median, it is imperative that you place the data in order first. It does not matter whether you order the data from smallest to largest or from largest to smallest, but it does matter that you order the data. Mode <span>Mode means fashion. The mode is the "most fashionable" number in a data set; it is the most frequently occurring score in a distribution and is used as a measure of central tendency. A set of data can have more than one mode, or even no mode. When all values are different, the data set has no mode. When a distribution has one value that appears most frequently, it i
Flashcard 1636635118860
| status | not learned | measured difficulty | 37% [default] | last interval [days] | |||
|---|---|---|---|---|---|---|---|
| repetition number in this series | 0 | memorised on | scheduled repetition | ||||
| scheduled repetition interval | last repetition or drill |
Subject 4. Measures of Center Tendency
ou order the data. Mode Mode means fashion. The mode is the "most fashionable" number in a data set; it is the most frequently occurring score in a distribution and is used as a measure of central tendency. <span>A set of data can have more than one mode, or even no mode. When all values are different, the data set has no mode. When a distribution has one value that appears most frequently, it is said to be unimodal. A data set that has two modes is said
Flashcard 1636637478156
| status | not learned | measured difficulty | 37% [default] | last interval [days] | |||
|---|---|---|---|---|---|---|---|
| repetition number in this series | 0 | memorised on | scheduled repetition | ||||
| scheduled repetition interval | last repetition or drill |
Subject 4. Measures of Center Tendency
fashion. The mode is the "most fashionable" number in a data set; it is the most frequently occurring score in a distribution and is used as a measure of central tendency. A set of data can have more than one mode, or even no mode. <span>When all values are different, the data set has no mode. When a distribution has one value that appears most frequently, it is said to be unimodal. A data set that has two modes is said to be bimodal. The advantage of the mode a
| status | not read | reprioritisations | ||
|---|---|---|---|---|
| last reprioritisation on | suggested re-reading day | |||
| started reading on | finished reading on |
Subject 4. Measures of Center Tendency
mber in a data set; it is the most frequently occurring score in a distribution and is used as a measure of central tendency. A set of data can have more than one mode, or even no mode. When all values are different, the data set has no mode. <span>When a distribution has one value that appears most frequently, it is said to be unimodal. A data set that has two modes is said to be bimodal. The advantage of the mode as a measure of central tendency is that its meaning is obvious. Like the median, the mode is not affected by extreme values. Further, it is the o
Flashcard 1636641410316
| status | not learned | measured difficulty | 37% [default] | last interval [days] | |||
|---|---|---|---|---|---|---|---|
| repetition number in this series | 0 | memorised on | scheduled repetition | ||||
| scheduled repetition interval | last repetition or drill |
Subject 4. Measures of Center Tendency
to be unimodal. A data set that has two modes is said to be bimodal. The advantage of the mode as a measure of central tendency is that its meaning is obvious. Like the median, the mode is not affected by extreme values. Further, <span>it is the only measure of central tendency that can be used with nominal data. The mode is greatly subject to sample fluctuations and, therefore, is not recommended for use as the only measure of central tendency. A further disadvantage of the mode is that many di
| status | not read | reprioritisations | ||
|---|---|---|---|---|
| last reprioritisation on | suggested re-reading day | |||
| started reading on | finished reading on |
Subject 4. Measures of Center Tendency
ons and, therefore, is not recommended for use as the only measure of central tendency. A further disadvantage of the mode is that many distributions have more than one mode. These distributions are called "multimodal." <span>Harmonic Mean The harmonic mean of n numbers x i (where i = 1, 2, ..., n) is: The special cases of n = 2 and n = 3 are given by: and so on. For n = 2, the harmonic mean is related to arithmetic mean A and geometric mean G by: The mean, median, and mode are equal in symmetric distributions. The mean is higher than the median in positively skewed distributions and lower than th
Flashcard 1636645342476
| status | not learned | measured difficulty | 37% [default] | last interval [days] | |||
|---|---|---|---|---|---|---|---|
| repetition number in this series | 0 | memorised on | scheduled repetition | ||||
| scheduled repetition interval | last repetition or drill |
Subject 4. Measures of Center Tendency
and so on. For n = 2, the harmonic mean is related to arithmetic mean A and geometric mean G by: The mean, median, and mode are equal in symmetric distributions. <span>The mean is higher than the median in positively skewed distributions and lower than the median in negatively skewed distributions. Extreme values affect the value of the mean, while the median is less affected by outliers. Mode helps to identify shape and skewness of distribution.<span><body><html>
Flashcard 1636647701772
| status | not learned | measured difficulty | 37% [default] | last interval [days] | |||
|---|---|---|---|---|---|---|---|
| repetition number in this series | 0 | memorised on | scheduled repetition | ||||
| scheduled repetition interval | last repetition or drill |
Subject 4. Measures of Center Tendency
and so on. For n = 2, the harmonic mean is related to arithmetic mean A and geometric mean G by: The mean, median, and mode are equal in symmetric distributions. <span>The mean is higher than the median in positively skewed distributions and lower than the median in negatively skewed distributions. Extreme values affect the value of the mean, while the median is less affected by outliers. Mode helps to identify shape and skewness of distribution.<span><body><html>
Flashcard 1636650061068
| status | not learned | measured difficulty | 37% [default] | last interval [days] | |||
|---|---|---|---|---|---|---|---|
| repetition number in this series | 0 | memorised on | scheduled repetition | ||||
| scheduled repetition interval | last repetition or drill |
Subject 4. Measures of Center Tendency
of n = 2 and n = 3 are given by: and so on. For n = 2, the harmonic mean is related to arithmetic mean A and geometric mean G by: <span>The mean, median, and mode are equal in symmetric distributions. The mean is higher than the median in positively skewed distributions and lower than the median in negatively skewed distributions. Extreme values affect the value of the mean, while th
Flashcard 1636652420364
| status | not learned | measured difficulty | 37% [default] | last interval [days] | |||
|---|---|---|---|---|---|---|---|
| repetition number in this series | 0 | memorised on | scheduled repetition | ||||
| scheduled repetition interval | last repetition or drill |
Subject 4. Measures of Center Tendency
ric distributions. The mean is higher than the median in positively skewed distributions and lower than the median in negatively skewed distributions. Extreme values affect the value of the mean, while the median is less affected by outliers. <span>Mode helps to identify shape and skewness of distribution.<span><body><html>
| status | not read | reprioritisations | ||
|---|---|---|---|---|
| last reprioritisation on | suggested re-reading day | |||
| started reading on | finished reading on |
| status | not read | reprioritisations | ||
|---|---|---|---|---|
| last reprioritisation on | suggested re-reading day | |||
| started reading on | finished reading on |
| status | not read | reprioritisations | ||
|---|---|---|---|---|
| last reprioritisation on | suggested re-reading day | |||
| started reading on | finished reading on |
Flashcard 1636667886860
| status | not learned | measured difficulty | 37% [default] | last interval [days] | |||
|---|---|---|---|---|---|---|---|
| repetition number in this series | 0 | memorised on | scheduled repetition | ||||
| scheduled repetition interval | last repetition or drill |
| status | not read | reprioritisations | ||
|---|---|---|---|---|
| last reprioritisation on | suggested re-reading day | |||
| started reading on | finished reading on |
Flashcard 1636817308940
| status | not learned | measured difficulty | 37% [default] | last interval [days] | |||
|---|---|---|---|---|---|---|---|
| repetition number in this series | 0 | memorised on | scheduled repetition | ||||
| scheduled repetition interval | last repetition or drill |
Parent (intermediate) annotation
Open itIn addition to permitting ranking and addition or subtraction, ratio scales allow computation of meaningful ratios.
Original toplevel document
Subject 2. Measurement Scaless in temperature, but a temperature of 30°F is not twice as warm as one of 15°F. Ratio Scale Ratio scales are like interval scales except that they have true zero points. This is the strongest measurement scale. <span>In addition to permitting ranking and addition or subtraction, ratio scales allow computation of meaningful ratios. A good example is the Kelvin scale of temperature. This scale has an absolute zero. Thus, a temperature of 300°K is twice as high as a temperature of 150°K. Two financial examples of ra
Flashcard 1636819668236
| status | not learned | measured difficulty | 37% [default] | last interval [days] | |||
|---|---|---|---|---|---|---|---|
| repetition number in this series | 0 | memorised on | scheduled repetition | ||||
| scheduled repetition interval | last repetition or drill |
Parent (intermediate) annotation
Open itIn a frequency distribution It is important to consider the number of intervals to be used. If too few intervals are used, too much data may be summarized and we may lose important characteristics; if too many intervals are used, we may not summarize enough.
Original toplevel document
Subject 3. Frequency Distributionsthat: Each observation can only lie in one interval. The total number of intervals will incorporate the whole population. The range for an interval is unique. This means a value (observation) can only fall into one interval. <span>It is important to consider the number of intervals to be used. If too few intervals are used, too much data may be summarized and we may lose important characteristics; if too many intervals are used, we may not summarize enough. A frequency distribution is constructed by dividing the scores into intervals and counting the number of scores in each interval. The actual number of scores and the percent
Flashcard 1636822027532
| status | not learned | measured difficulty | 37% [default] | last interval [days] | |||
|---|---|---|---|---|---|---|---|
| repetition number in this series | 0 | memorised on | scheduled repetition | ||||
| scheduled repetition interval | last repetition or drill |
Parent (intermediate) annotation
Open itIn a frequency distribution It is important to consider the number of intervals to be used. If too few intervals are used, too much data may be summarized and we may lose important characteristics; if too many intervals are used, we may not summarize enough.
Original toplevel document
Subject 3. Frequency Distributionsthat: Each observation can only lie in one interval. The total number of intervals will incorporate the whole population. The range for an interval is unique. This means a value (observation) can only fall into one interval. <span>It is important to consider the number of intervals to be used. If too few intervals are used, too much data may be summarized and we may lose important characteristics; if too many intervals are used, we may not summarize enough. A frequency distribution is constructed by dividing the scores into intervals and counting the number of scores in each interval. The actual number of scores and the percent
Flashcard 1636824386828
| status | not learned | measured difficulty | 37% [default] | last interval [days] | |||
|---|---|---|---|---|---|---|---|
| repetition number in this series | 0 | memorised on | scheduled repetition | ||||
| scheduled repetition interval | last repetition or drill |
Parent (intermediate) annotation
Open itIn a frequency distribution It is important to consider the number of intervals to be used. If too few intervals are used, too much data may be summarized and we may lose important characteristics; if too many intervals are used, we may not summarize enough.
Original toplevel document
Subject 3. Frequency Distributionsthat: Each observation can only lie in one interval. The total number of intervals will incorporate the whole population. The range for an interval is unique. This means a value (observation) can only fall into one interval. <span>It is important to consider the number of intervals to be used. If too few intervals are used, too much data may be summarized and we may lose important characteristics; if too many intervals are used, we may not summarize enough. A frequency distribution is constructed by dividing the scores into intervals and counting the number of scores in each interval. The actual number of scores and the percent
Flashcard 1636826221836
| status | not learned | measured difficulty | 37% [default] | last interval [days] | |||
|---|---|---|---|---|---|---|---|
| repetition number in this series | 0 | memorised on | scheduled repetition | ||||
| scheduled repetition interval | last repetition or drill |
Parent (intermediate) annotation
Open itThe following steps are required when organizing data into a frequency distribution together with suggestions on constructing the frequency distribution. Identify the highest and lowest values of the observations. Setup classes (groups into which data is divided). The classes must be mutually exclusive and of equal size. Add up the number of observations and assign
Original toplevel document
Subject 3. Frequency Distributionsby the total number of observations. Cumulative absolute frequency and cumulative relative frequency are the results from cumulating the absolute and relative frequencies as we move from the first to the last interval. <span>The following steps are required when organizing data into a frequency distribution together with suggestions on constructing the frequency distribution. Identify the highest and lowest values of the observations. Setup classes (groups into which data is divided). The classes must be mutually exclusive and of equal size. Add up the number of observations and assign each observation to its class. Count the number of observations in each class. This is called the class frequency. Data can be divided into two types: discrete and continuous. Discrete: The values in the data set can be counted. There are distinct spaces between the values, such as
Flashcard 1636828581132
| status | not learned | measured difficulty | 37% [default] | last interval [days] | |||
|---|---|---|---|---|---|---|---|
| repetition number in this series | 0 | memorised on | scheduled repetition | ||||
| scheduled repetition interval | last repetition or drill |
Parent (intermediate) annotation
Open itThe following steps are required when organizing data into a frequency distribution together with suggestions on constructing the frequency distribution. Identify the highest and lowest values of the observations. Setup classes (groups into which data is divided). The classes must be mutually exclusive and of equal size. Add up the number of observations and assign
Original toplevel document
Subject 3. Frequency Distributionsby the total number of observations. Cumulative absolute frequency and cumulative relative frequency are the results from cumulating the absolute and relative frequencies as we move from the first to the last interval. <span>The following steps are required when organizing data into a frequency distribution together with suggestions on constructing the frequency distribution. Identify the highest and lowest values of the observations. Setup classes (groups into which data is divided). The classes must be mutually exclusive and of equal size. Add up the number of observations and assign each observation to its class. Count the number of observations in each class. This is called the class frequency. Data can be divided into two types: discrete and continuous. Discrete: The values in the data set can be counted. There are distinct spaces between the values, such as
Flashcard 1636830416140
| status | not learned | measured difficulty | 37% [default] | last interval [days] | |||
|---|---|---|---|---|---|---|---|
| repetition number in this series | 0 | memorised on | scheduled repetition | ||||
| scheduled repetition interval | last repetition or drill |
Parent (intermediate) annotation
Open itThe following steps are required when organizing data into a frequency distribution together with suggestions on constructing the frequency distribution. Identify the highest and lowest values of the observations. Setup classes (groups into which data is divided). The classes must be mutually exclusive and of equal size. Add up the number of observations and assign
Original toplevel document
Subject 3. Frequency Distributionsby the total number of observations. Cumulative absolute frequency and cumulative relative frequency are the results from cumulating the absolute and relative frequencies as we move from the first to the last interval. <span>The following steps are required when organizing data into a frequency distribution together with suggestions on constructing the frequency distribution. Identify the highest and lowest values of the observations. Setup classes (groups into which data is divided). The classes must be mutually exclusive and of equal size. Add up the number of observations and assign each observation to its class. Count the number of observations in each class. This is called the class frequency. Data can be divided into two types: discrete and continuous. Discrete: The values in the data set can be counted. There are distinct spaces between the values, such as
Flashcard 1636832251148
| status | not learned | measured difficulty | 37% [default] | last interval [days] | |||
|---|---|---|---|---|---|---|---|
| repetition number in this series | 0 | memorised on | scheduled repetition | ||||
| scheduled repetition interval | last repetition or drill |
Parent (intermediate) annotation
Open itThe following steps are required when organizing data into a frequency distribution together with suggestions on constructing the frequency distribution. Identify the highest and lowest values of the observations. Setup classes (groups into which data is divided). The classes must be mutually exclusive and of equal size. Add up the number of observations and assign
Original toplevel document
Subject 3. Frequency Distributionsby the total number of observations. Cumulative absolute frequency and cumulative relative frequency are the results from cumulating the absolute and relative frequencies as we move from the first to the last interval. <span>The following steps are required when organizing data into a frequency distribution together with suggestions on constructing the frequency distribution. Identify the highest and lowest values of the observations. Setup classes (groups into which data is divided). The classes must be mutually exclusive and of equal size. Add up the number of observations and assign each observation to its class. Count the number of observations in each class. This is called the class frequency. Data can be divided into two types: discrete and continuous. Discrete: The values in the data set can be counted. There are distinct spaces between the values, such as
Flashcard 1636834086156
| status | not learned | measured difficulty | 37% [default] | last interval [days] | |||
|---|---|---|---|---|---|---|---|
| repetition number in this series | 0 | memorised on | scheduled repetition | ||||
| scheduled repetition interval | last repetition or drill |
Parent (intermediate) annotation
Open itdata into a frequency distribution together with suggestions on constructing the frequency distribution. Identify the highest and lowest values of the observations. Setup classes (groups into which data is divided). <span>The classes must be mutually exclusive and of equal size. Add up the number of observations and assign each observation to its class. Count the number of observations in each class. This is called the class freque
Original toplevel document
Subject 3. Frequency Distributionsby the total number of observations. Cumulative absolute frequency and cumulative relative frequency are the results from cumulating the absolute and relative frequencies as we move from the first to the last interval. <span>The following steps are required when organizing data into a frequency distribution together with suggestions on constructing the frequency distribution. Identify the highest and lowest values of the observations. Setup classes (groups into which data is divided). The classes must be mutually exclusive and of equal size. Add up the number of observations and assign each observation to its class. Count the number of observations in each class. This is called the class frequency. Data can be divided into two types: discrete and continuous. Discrete: The values in the data set can be counted. There are distinct spaces between the values, such as
Flashcard 1636837231884
| status | not learned | measured difficulty | 37% [default] | last interval [days] | |||
|---|---|---|---|---|---|---|---|
| repetition number in this series | 0 | memorised on | scheduled repetition | ||||
| scheduled repetition interval | last repetition or drill |
Parent (intermediate) annotation
Open ittions. Setup classes (groups into which data is divided). The classes must be mutually exclusive and of equal size. Add up the number of observations and assign each observation to its class. Count <span>the number of observations in each class. This is called the class frequency.<span><body><html>
Original toplevel document
Subject 3. Frequency Distributionsby the total number of observations. Cumulative absolute frequency and cumulative relative frequency are the results from cumulating the absolute and relative frequencies as we move from the first to the last interval. <span>The following steps are required when organizing data into a frequency distribution together with suggestions on constructing the frequency distribution. Identify the highest and lowest values of the observations. Setup classes (groups into which data is divided). The classes must be mutually exclusive and of equal size. Add up the number of observations and assign each observation to its class. Count the number of observations in each class. This is called the class frequency. Data can be divided into two types: discrete and continuous. Discrete: The values in the data set can be counted. There are distinct spaces between the values, such as
Flashcard 1636857941260
| status | not learned | measured difficulty | 37% [default] | last interval [days] | |||
|---|---|---|---|---|---|---|---|
| repetition number in this series | 0 | memorised on | scheduled repetition | ||||
| scheduled repetition interval | last repetition or drill |
Flashcard 1636859776268
| status | not learned | measured difficulty | 37% [default] | last interval [days] | |||
|---|---|---|---|---|---|---|---|
| repetition number in this series | 0 | memorised on | scheduled repetition | ||||
| scheduled repetition interval | last repetition or drill |
Flashcard 1636861611276
| status | not learned | measured difficulty | 37% [default] | last interval [days] | |||
|---|---|---|---|---|---|---|---|
| repetition number in this series | 0 | memorised on | scheduled repetition | ||||
| scheduled repetition interval | last repetition or drill |
Flashcard 1636864232716
| status | not learned | measured difficulty | 37% [default] | last interval [days] | |||
|---|---|---|---|---|---|---|---|
| repetition number in this series | 0 | memorised on | scheduled repetition | ||||
| scheduled repetition interval | last repetition or drill |
Flashcard 1636866067724
| status | not learned | measured difficulty | 37% [default] | last interval [days] | |||
|---|---|---|---|---|---|---|---|
| repetition number in this series | 0 | memorised on | scheduled repetition | ||||
| scheduled repetition interval | last repetition or drill |
Flashcard 1636867902732
| status | not learned | measured difficulty | 37% [default] | last interval [days] | |||
|---|---|---|---|---|---|---|---|
| repetition number in this series | 0 | memorised on | scheduled repetition | ||||
| scheduled repetition interval | last repetition or drill |
Flashcard 1636869999884
| status | not learned | measured difficulty | 37% [default] | last interval [days] | |||
|---|---|---|---|---|---|---|---|
| repetition number in this series | 0 | memorised on | scheduled repetition | ||||
| scheduled repetition interval | last repetition or drill |
Flashcard 1636871834892
| status | not learned | measured difficulty | 37% [default] | last interval [days] | |||
|---|---|---|---|---|---|---|---|
| repetition number in this series | 0 | memorised on | scheduled repetition | ||||
| scheduled repetition interval | last repetition or drill |
Flashcard 1636873669900
| status | not learned | measured difficulty | 37% [default] | last interval [days] | |||
|---|---|---|---|---|---|---|---|
| repetition number in this series | 0 | memorised on | scheduled repetition | ||||
| scheduled repetition interval | last repetition or drill |
Flashcard 1636875504908
| status | not learned | measured difficulty | 37% [default] | last interval [days] | |||
|---|---|---|---|---|---|---|---|
| repetition number in this series | 0 | memorised on | scheduled repetition | ||||
| scheduled repetition interval | last repetition or drill |
Flashcard 1636877339916
| status | not learned | measured difficulty | 37% [default] | last interval [days] | |||
|---|---|---|---|---|---|---|---|
| repetition number in this series | 0 | memorised on | scheduled repetition | ||||
| scheduled repetition interval | last repetition or drill |
Flashcard 1636879174924
| status | not learned | measured difficulty | 37% [default] | last interval [days] | |||
|---|---|---|---|---|---|---|---|
| repetition number in this series | 0 | memorised on | scheduled repetition | ||||
| scheduled repetition interval | last repetition or drill |
Flashcard 1636948905228
| status | not learned | measured difficulty | 37% [default] | last interval [days] | |||
|---|---|---|---|---|---|---|---|
| repetition number in this series | 0 | memorised on | scheduled repetition | ||||
| scheduled repetition interval | last repetition or drill |
Flashcard 1637079452940
| status | not learned | measured difficulty | 37% [default] | last interval [days] | |||
|---|---|---|---|---|---|---|---|
| repetition number in this series | 0 | memorised on | scheduled repetition | ||||
| scheduled repetition interval | last repetition or drill |
Flashcard 1637115890956
| status | not learned | measured difficulty | 37% [default] | last interval [days] | |||
|---|---|---|---|---|---|---|---|
| repetition number in this series | 0 | memorised on | scheduled repetition | ||||
| scheduled repetition interval | last repetition or drill |
Flashcard 1637146299660
| status | not learned | measured difficulty | 37% [default] | last interval [days] | |||
|---|---|---|---|---|---|---|---|
| repetition number in this series | 0 | memorised on | scheduled repetition | ||||
| scheduled repetition interval | last repetition or drill |
Flashcard 1637148134668
| status | not learned | measured difficulty | 37% [default] | last interval [days] | |||
|---|---|---|---|---|---|---|---|
| repetition number in this series | 0 | memorised on | scheduled repetition | ||||
| scheduled repetition interval | last repetition or drill |
Flashcard 1637149969676
| status | not learned | measured difficulty | 37% [default] | last interval [days] | |||
|---|---|---|---|---|---|---|---|
| repetition number in this series | 0 | memorised on | scheduled repetition | ||||
| scheduled repetition interval | last repetition or drill |
Flashcard 1637151804684
| status | not learned | measured difficulty | 37% [default] | last interval [days] | |||
|---|---|---|---|---|---|---|---|
| repetition number in this series | 0 | memorised on | scheduled repetition | ||||
| scheduled repetition interval | last repetition or drill |
Flashcard 1637153639692
| status | not learned | measured difficulty | 37% [default] | last interval [days] | |||
|---|---|---|---|---|---|---|---|
| repetition number in this series | 0 | memorised on | scheduled repetition | ||||
| scheduled repetition interval | last repetition or drill |
Flashcard 1637155736844
| status | not learned | measured difficulty | 37% [default] | last interval [days] | |||
|---|---|---|---|---|---|---|---|
| repetition number in this series | 0 | memorised on | scheduled repetition | ||||
| scheduled repetition interval | last repetition or drill |
| status | not read | reprioritisations | ||
|---|---|---|---|---|
| last reprioritisation on | suggested re-reading day | |||
| started reading on | finished reading on |
Flashcard 1637159144716
| status | not learned | measured difficulty | 37% [default] | last interval [days] | |||
|---|---|---|---|---|---|---|---|
| repetition number in this series | 0 | memorised on | scheduled repetition | ||||
| scheduled repetition interval | last repetition or drill |
Flashcard 1637161766156
| status | not learned | measured difficulty | 37% [default] | last interval [days] | |||
|---|---|---|---|---|---|---|---|
| repetition number in this series | 0 | memorised on | scheduled repetition | ||||
| scheduled repetition interval | last repetition or drill |
| status | not read | reprioritisations | ||
|---|---|---|---|---|
| last reprioritisation on | suggested re-reading day | |||
| started reading on | finished reading on |
| status | not read | reprioritisations | ||
|---|---|---|---|---|
| last reprioritisation on | suggested re-reading day | |||
| started reading on | finished reading on |
Flashcard 1637167795468
| status | not learned | measured difficulty | 37% [default] | last interval [days] | |||
|---|---|---|---|---|---|---|---|
| repetition number in this series | 0 | memorised on | scheduled repetition | ||||
| scheduled repetition interval | last repetition or drill |
Parent (intermediate) annotation
Open itts of decimal places involved and (theoretically, at least) there are no gaps between permissible values (i.e., all values can be included in the data set). Examples would include the height of a person and the time to complete an assignment. <span>These values can be measured using sufficiently accurate tools to numerous decimal places.<span><body><html>
Original toplevel document
Subject 3. Frequency Distributionsed into two types: discrete and continuous. Discrete: The values in the data set can be counted. There are distinct spaces between the values, such as the number of children in a family or the number of shares comprising an index. <span>Continuous: The values in the data set can be measured. There are normally lots of decimal places involved and (theoretically, at least) there are no gaps between permissible values (i.e., all values can be included in the data set). Examples would include the height of a person and the time to complete an assignment. These values can be measured using sufficiently accurate tools to numerous decimal places. There are two methods that graphically represent continuous data: histograms and frequency polygons. 1. A histogram is a bar chart that displays a frequency distributi
Flashcard 1637170154764
| status | not learned | measured difficulty | 37% [default] | last interval [days] | |||
|---|---|---|---|---|---|---|---|
| repetition number in this series | 0 | memorised on | scheduled repetition | ||||
| scheduled repetition interval | last repetition or drill |
Parent (intermediate) annotation
Open itan>Continuous: The values in the data set can be measured. There are normally lots of decimal places involved and (theoretically, at least) there are no gaps between permissible values (i.e., all values can be included in the data set). Examples would include the height of a person and the time to complete an assignment. These values can be measured using sufficiently accurate tools to numerous decimal places.<span><body><html>
Original toplevel document
Subject 3. Frequency Distributionsed into two types: discrete and continuous. Discrete: The values in the data set can be counted. There are distinct spaces between the values, such as the number of children in a family or the number of shares comprising an index. <span>Continuous: The values in the data set can be measured. There are normally lots of decimal places involved and (theoretically, at least) there are no gaps between permissible values (i.e., all values can be included in the data set). Examples would include the height of a person and the time to complete an assignment. These values can be measured using sufficiently accurate tools to numerous decimal places. There are two methods that graphically represent continuous data: histograms and frequency polygons. 1. A histogram is a bar chart that displays a frequency distributi
Flashcard 1637172514060
| status | not learned | measured difficulty | 37% [default] | last interval [days] | |||
|---|---|---|---|---|---|---|---|
| repetition number in this series | 0 | memorised on | scheduled repetition | ||||
| scheduled repetition interval | last repetition or drill |
Parent (intermediate) annotation
Open itContinuous: The values in the data set can be measured. There are normally lots of decimal places involved and (theoretically, at least) there are no gaps between permissible values (i.e., all values can be included in the data set). Example
Original toplevel document
Subject 3. Frequency Distributionsed into two types: discrete and continuous. Discrete: The values in the data set can be counted. There are distinct spaces between the values, such as the number of children in a family or the number of shares comprising an index. <span>Continuous: The values in the data set can be measured. There are normally lots of decimal places involved and (theoretically, at least) there are no gaps between permissible values (i.e., all values can be included in the data set). Examples would include the height of a person and the time to complete an assignment. These values can be measured using sufficiently accurate tools to numerous decimal places. There are two methods that graphically represent continuous data: histograms and frequency polygons. 1. A histogram is a bar chart that displays a frequency distributi
| status | not read | reprioritisations | ||
|---|---|---|---|---|
| last reprioritisation on | suggested re-reading day | |||
| started reading on | finished reading on |
| status | not read | reprioritisations | ||
|---|---|---|---|---|
| last reprioritisation on | suggested re-reading day | |||
| started reading on | finished reading on |
| status | not read | reprioritisations | ||
|---|---|---|---|---|
| last reprioritisation on | suggested re-reading day | |||
| started reading on | finished reading on |
| status | not read | reprioritisations | ||
|---|---|---|---|---|
| last reprioritisation on | suggested re-reading day | |||
| started reading on | finished reading on |
| status | not read | reprioritisations | ||
|---|---|---|---|---|
| last reprioritisation on | suggested re-reading day | |||
| started reading on | finished reading on |
| status | not read | reprioritisations | ||
|---|---|---|---|---|
| last reprioritisation on | suggested re-reading day | |||
| started reading on | finished reading on |
| status | not read | reprioritisations | ||
|---|---|---|---|---|
| last reprioritisation on | suggested re-reading day | |||
| started reading on | finished reading on |
| status | not read | reprioritisations | ||
|---|---|---|---|---|
| last reprioritisation on | suggested re-reading day | |||
| started reading on | finished reading on |
| status | not read | reprioritisations | ||
|---|---|---|---|---|
| last reprioritisation on | suggested re-reading day | |||
| started reading on | finished reading on |
Flashcard 1637191650572
| status | not learned | measured difficulty | 37% [default] | last interval [days] | |||
|---|---|---|---|---|---|---|---|
| repetition number in this series | 0 | memorised on | scheduled repetition | ||||
| scheduled repetition interval | last repetition or drill |
| status | not read | reprioritisations | ||
|---|---|---|---|---|
| last reprioritisation on | suggested re-reading day | |||
| started reading on | finished reading on |
Flashcard 1637195058444
| status | not learned | measured difficulty | 37% [default] | last interval [days] | |||
|---|---|---|---|---|---|---|---|
| repetition number in this series | 0 | memorised on | scheduled repetition | ||||
| scheduled repetition interval | last repetition or drill |
Flashcard 1637196893452
| status | not learned | measured difficulty | 37% [default] | last interval [days] | |||
|---|---|---|---|---|---|---|---|
| repetition number in this series | 0 | memorised on | scheduled repetition | ||||
| scheduled repetition interval | last repetition or drill |
Flashcard 1637198728460
| status | not learned | measured difficulty | 37% [default] | last interval [days] | |||
|---|---|---|---|---|---|---|---|
| repetition number in this series | 0 | memorised on | scheduled repetition | ||||
| scheduled repetition interval | last repetition or drill |
| status | not read | reprioritisations | ||
|---|---|---|---|---|
| last reprioritisation on | suggested re-reading day | |||
| started reading on | finished reading on |
Flashcard 1637202922764
| status | not learned | measured difficulty | 37% [default] | last interval [days] | |||
|---|---|---|---|---|---|---|---|
| repetition number in this series | 0 | memorised on | scheduled repetition | ||||
| scheduled repetition interval | last repetition or drill |
| status | not read | reprioritisations | ||
|---|---|---|---|---|
| last reprioritisation on | suggested re-reading day | |||
| started reading on | finished reading on |
Flashcard 1637206592780
| status | not learned | measured difficulty | 37% [default] | last interval [days] | |||
|---|---|---|---|---|---|---|---|
| repetition number in this series | 0 | memorised on | scheduled repetition | ||||
| scheduled repetition interval | last repetition or drill |
Flashcard 1637208427788
| status | not learned | measured difficulty | 37% [default] | last interval [days] | |||
|---|---|---|---|---|---|---|---|
| repetition number in this series | 0 | memorised on | scheduled repetition | ||||
| scheduled repetition interval | last repetition or drill |
Flashcard 1637210524940
| status | not learned | measured difficulty | 37% [default] | last interval [days] | |||
|---|---|---|---|---|---|---|---|
| repetition number in this series | 0 | memorised on | scheduled repetition | ||||
| scheduled repetition interval | last repetition or drill |
| status | not read | reprioritisations | ||
|---|---|---|---|---|
| last reprioritisation on | suggested re-reading day | |||
| started reading on | finished reading on |
Flashcard 1637214457100
| status | not learned | measured difficulty | 37% [default] | last interval [days] | |||
|---|---|---|---|---|---|---|---|
| repetition number in this series | 0 | memorised on | scheduled repetition | ||||
| scheduled repetition interval | last repetition or drill |
Flashcard 1637216292108
| status | not learned | measured difficulty | 37% [default] | last interval [days] | |||
|---|---|---|---|---|---|---|---|
| repetition number in this series | 0 | memorised on | scheduled repetition | ||||
| scheduled repetition interval | last repetition or drill |
Flashcard 1637218127116
| status | not learned | measured difficulty | 37% [default] | last interval [days] | |||
|---|---|---|---|---|---|---|---|
| repetition number in this series | 0 | memorised on | scheduled repetition | ||||
| scheduled repetition interval | last repetition or drill |
| status | not read | reprioritisations | ||
|---|---|---|---|---|
| last reprioritisation on | suggested re-reading day | |||
| started reading on | finished reading on |
| status | not read | reprioritisations | ||
|---|---|---|---|---|
| last reprioritisation on | suggested re-reading day | |||
| started reading on | finished reading on |
| status | not read | reprioritisations | ||
|---|---|---|---|---|
| last reprioritisation on | suggested re-reading day | |||
| started reading on | finished reading on |
| status | not read | reprioritisations | ||
|---|---|---|---|---|
| last reprioritisation on | suggested re-reading day | |||
| started reading on | finished reading on |
| status | not read | reprioritisations | ||
|---|---|---|---|---|
| last reprioritisation on | suggested re-reading day | |||
| started reading on | finished reading on |